対称化された配列

対称性のある配列の表現歪対称配列
対称化された配列の構築
対称性は，高階のテンソルの扱いにおいて重要な役割を果たす．物理学や数学で重要な高階のテンソルは，対称慣性テンソルから四階剛性テンソルや曲率テンソル等のように対称性を持っている．その多くは転置対称性を持っているが，かなり複雑なこともある．Wolframシステムは任意の階数あるいは次元のテンソルの置換対称性に対する完全な言語を実装しており，対称性による独立成分だけを保存する特殊な配列を提供する．これにはより複雑なアルゴリズムが要求されるので，通常の速さを犠牲にするが，それでも大きな記憶空間が必要となることがよくある．対称性については「テンソルの対称性」で説明してある．
対称性のある配列の表現
SymmetrizedArray
対称の独立要素のみを保存する配列を構築する
SymmetrizedArrayRules
対称化された配列の独立成分の規則のリスト
SymmetrizedReplacePart
対称化された配列の独立成分を交換する
対称化された配列
次は対称性を持つ配列である：
つまり，この配列はそのスロットのすべての置換の下で不変である：
もっと簡単な方法で保存することができる．この方が，何回も繰り返されている要素がいくつかあるということが分かりやすい：
新しい表現には，次元，非零の独立成分と対称性のリストが含まれる：
その正規形はもとの配列と偶然一致している：
配列の独立要素に対して規則がある．最後のデフォルトの規則はここで与えられていない独立成分は値0を取るということを表している：
対称化された配列では，対称性を含むいくつかの配列をコンパクトに保存することができる．特に反対称の配列では利点が最大になる．最も極端な非ゼロ配列の場合，次元 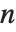の 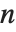階完全反対称配列には1つの独立成分がある．その疎配列には 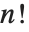個の非ゼロ要素が，その正規形には 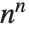個の項目がある．ところが，対称化された配列の操作はより複雑なアルゴリズムを必要とするので，通常操作は遅くなる．
LeviCivitaTensorはデフォルトで疎な表現を返す：
LeviCivitaTensorは対称化された正規の表現を提供する：
いろいろな表現方法の大きさを比較する：
Wolframシステムには他にも高対称の配列がある：
StructuredArrayオブジェクトは原子オブジェクトとして扱われる．その情報は関数を使ってアクセスすることができる．
対称化された配列は原子的である：
配列についての情報は，次のようにして得ることができる：
独立かどうかにかかわらず，配列の厳密成分である：
可能な限り対称性を維持して，部分配列を抽出する：
個々の要素は変更することができる．与えられた規則は，それに対応する独立成分の規則に変換される：
対称化された配列の構築
SymmetrizedArrayを使うとより効率的な形式で対称性のある通常の配列を書き換えることができるということが分かっている．SparseArray，SymmetrizedArrayに従っても，規則のリストや対称性指定から同様に効率的な表現が構築できる．
歪対称行列のSymmetrizedArray形式：
以下はその独立成分である：
これらの規則と対称性から配列を再構築する：
対称性が与えられないと，恒等対称性が想定される．結果は同じ規則でSparseArrayを使ったときと同じである：
対称性と互換でない規則は無視される：
SymmetrizedArrayの第1引数の規則に一般的なパターンを使うことができる．これらの規則はSymmetrizedIndependentComponentsによって与えられるように独立成分のみの規則であり，SparseArrayで与えられるような配列のすべての位置に対するものではない．特に，これは乱数の項目で対称化された配列を生成するのに便利である．
四次元のランダムな階数3の歪対称配列：
配列の成分として，指標の付いた式を使う：
対称化された配列を構築する別の方法として，関数Symmetrizeを使った別の配列の実際の対称化によるものがある．
一般的な行列を対称化する：
他の対称性で対称化する：
歪対称配列
歪対称テンソルは，外積代数で基本的な役割を果たす．Wolframシステムは歪対称テンソルとホッジ双対性のウェッジ積の基本的操作を提供する．
五次元の歪対称配列を2つ取る：
これらのウェッジ積は，階数の多項式によって与えられる乗法因子を除いて，歪対称化されたテンソル積である：
合計の階数が次元を上回ると結果は消失する：
SymmetrizedArray表現を使うと高次元でも扱える．これは通常の表現や疎な表現では不可能である：
結果は，そのホッジ双対性を与え，より便利に表現される：