对称数组

具有对称性的数组的表示法反对称数组
构建对称数组
对称性在处理高阶张量上发挥重要作用. 物理和数学中绝大多数重要的高阶张量具有对称性，从对称惯性张量到阶数为4的刚性和曲率张量. 它们当中大多数都有转置对称性，在某些情况下，还相当复杂. Wolfram 系统实现了完整的任意阶数或者维度的张量的置换对称性的语言，并且提供了只存储关于对称性的独立分量的专门数组类型. 这常常导致存储空间显著增大，虽然通常以较慢的操作为代价，因为需要更复杂的算法. 参见 "张量对称性" 以获取对称性语言的描述.
具有对称性的数组的表示法
SymmetrizedArray
构建只存储对称独立分量的数组
SymmetrizedArrayRules
对称数组的独立分量组成的规则列表
SymmetrizedReplacePart
在对称数组中替换独立分量
对称数组.
这是一个具有对称性的数组：
这表示在位置的所有置换下，数组是不变的：
它可以用更简单的方式存储，这更好地反映了某些元素多次重复的事实：
新的表示法包含维度、非零独立分量列表和对称性：
正则形式与原始数组保持一致：
这些是数组的独立分量的规则. 最后的默认规则表示这里给出的独立分量的值不能是0：
对称数组提供了紧凑的方法来存储具有相当大对称性的数组. 特别地，反对称性最大化了这个有点. 在极端的非零情况下，在维度为 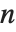的空间中阶数为 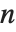的反对称数组具有一个独立分量. 它的稀疏表示法包含 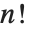个非零元素，而它的正则形式有 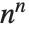个元素. 另一种情况，对称数组的操作通常较慢，因为它需要更复杂的算法.
默认情况下，LeviCivitaTensor 提供了稀疏表示法：
LeviCivitaTensor 提供对称和正常表示：
比较不同表示法的规模：
Wolfram 系统中有其他高度对称的数组：
SymmetrizedArray 对象视为原子对象. 它们的信息可以使用函数访问.
对称数组是原子的：
关于数组的信息可以按下列方法获得：
提取数组的分量，与它们是否独立无关：
提取子数组，如果可能保持对称性：
单个元素可以被改变. 注意，给定规则被转化为相应的独立分量规则：
构建对称数组
已经证明，SymmetrizedArray 可用于以更有效的形式重写具有对称性的正则数组. 遵循 SparseArray， SymmetrizedArray 也可以从规则列表和对称性指定构建同样有效的表示法.
反对称矩阵的 SymmetrizedArray 形式：
这写是它的独立分量：
从这些规则和对称性，重新构建数组：
如果不提供对称性，那么假定采用恒等对称性. 该结果与在相同规则下使用 SparseArray 等价：
忽略与对称性不兼容的规则：
规则中的常见模式可以用于 SymmetrizedArray 的第一个参数中. 这些规则是只用于独立分量的规则，正如SymmetrizedIndependentComponents 给出的，并且不像 SparseArray 是用于数组的所有位置的. 特别地，这对于生成具有随机元素的对称数组很有用.
维度为4的空间中阶数为3的随机反对称数组：
将索引表达式作为数组分量使用：
另一种构建对称数组的方式实际上是其他数组的对称化，使用函数 Symmetrize.
对称化一个普通矩阵：
使用其他对称性进行对称化：
反对称数组
反对称张量在外部代数发挥了重要的作用. Wolfram 系统提供了反对称张量和霍奇对偶性组成的 wedge 乘积的基本操作.
采取维度5中的两个反对称数组：
它们的 wedge 乘积是反对称张量乘积，除了由任意的多项给出的乘数因子：
当总阶数超过维度，结果化为零：
SymmetrizedArray 表示法允许作用于高维度；否则，可能无法用于正常或者稀疏表示法：
给出霍奇对偶，可以更方便地表示结果：