ArrayReduce

ArrayReduce[f,array,n]

reduces dimension n of array by applying f.

ArrayReduce[f,array,n1;;n2]

reduces dimensions n1 through n2.

ArrayReduce[f,array,{n1,n2,…}]

reduces dimensions n1, n2, etc.

ArrayReduce[f,array,{{n11,n12,…},{n21,n22,…},…}]

applies f to arrays formed by combining all dimensions nij to make each dimension i.

Details

  • Array reduction, also called array aggregation, is used to compute functions such as Mean, Total or StandardDeviation along specific dimensions of an array.
  • In ArrayReduce[f,array,n], f is applied to every vector along the n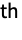^(th) dimension of array. It can be seen as a transposition where dimension n becomes the last dimension, followed by the application of f on the lowest-level vectors:
  • If array has dimensions {d1,d2,…}, and if the function is transforming a vector into a scalar, the results is an array that has the same dimensions as array except for dn, which is dropped.
  • In ArrayReduce[f,array,n1;;n2] and ArrayReduce[f,array,{n1,n2,…}], f is applied to every vector formed by combining and flattening the specified dimensions.
  • In ArrayReduce[f,array,{{n11,n12,…},{n21,n22,…},…}], f is applied to arrays of arbitrary ranks instead of vectors only.
  • ArrayReduce[f,array,{n1,n2,…}] is equivalent to ArrayReduce[f,array,{{n1,n2,…}}].

Examples

Basic Examples  (3)

Compute the mean of every row of a matrix:

Compute the mean of every column of a matrix:

Define an array of rank 3:

Compute the standard deviation over the second dimension:

The resulting array is of rank 2, and the second axis has been removed:

Visualize the input and output arrays:

Define an array of rank 5:

Reduce the dimensions of the array by computing the total over dimensions 2 and 4:

Wolfram Research (2020), ArrayReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayReduce.html.

Text

Wolfram Research (2020), ArrayReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayReduce.html.

CMS

Wolfram Language. 2020. "ArrayReduce." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayReduce.html.

APA

Wolfram Language. (2020). ArrayReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayReduce.html

BibTeX

@misc{reference.wolfram_2024_arrayreduce, author="Wolfram Research", title="{ArrayReduce}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayReduce.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arrayreduce, organization={Wolfram Research}, title={ArrayReduce}, year={2020}, url={https://reference.wolfram.com/language/ref/ArrayReduce.html}, note=[Accessed: 22-December-2024 ]}