CauchyMatrix[x,y]
represents the Cauchy matrix given by the generating vectors x and y as a structured array.
CauchyMatrix[x]
is equivalent to CauchyMatrix[x,x].
CauchyMatrix[cmat]
converts a Cauchy matrix cmat to a structured array.


CauchyMatrix
CauchyMatrix[x,y]
represents the Cauchy matrix given by the generating vectors x and y as a structured array.
CauchyMatrix[x]
is equivalent to CauchyMatrix[x,x].
CauchyMatrix[cmat]
converts a Cauchy matrix cmat to a structured array.
Details and Options


- Cauchy matrices, when represented as structured arrays, allow for efficient storage and more efficient operations, including Det, Inverse and LinearSolve.
- Cauchy matrices occur in computations related to rational interpolation, conformal mappings, n-body simulations and the discretization of integral equations with singular kernels.
- Given generating vectors x and y, the resulting Cauchy matrix
 has entries given by
has entries given by 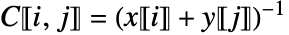 .
. - Operations that are accelerated for CauchyMatrix include:
-
Det time 
Inverse time 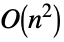
LinearSolve time 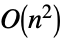
- For a CauchyMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"XVector" generating vector x "YVector" generating vector y "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[CauchyMatrix[x]] gives the Cauchy matrix as an ordinary matrix.
- CauchyMatrix[…,TargetStructure->struct] returns the Cauchy matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Structured" represent the matrix as a structured array "Symmetric" represent the matrix as a symmetric matrix - CauchyMatrix[…,TargetStructureAutomatic] is equivalent to CauchyMatrix[…,TargetStructure"Structured"].
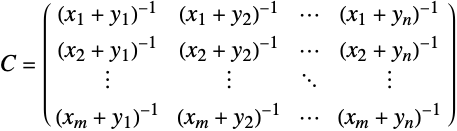
Examples
open all close allBasic Examples (2)
Normal can convert a CauchyMatrix to its ordinary representation:
Scope (6)
Generate a symmetric Cauchy matrix:
Get the normal representation:
Generate a rectangular Cauchy matrix:
Get the normal representation:
Represent a dense Cauchy matrix as a structured array:
The structured representation typically uses much less memory:
CauchyMatrix objects include properties that give information about the array:
The "XVector" and "YVector" properties give the generating vectors of the Cauchy matrix:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
When appropriate, structured algorithms return another CauchyMatrix object:
The transpose is also a CauchyMatrix:
The product of a Cauchy matrix and its transpose is no longer a Cauchy matrix:
Options (1)
Applications (3)
Represent the Hilbert matrix as a CauchyMatrix:
Compare with HilbertMatrix:
Numerically compute the inverse for a large Hilbert matrix:

The result from the structured version is more accurate:
Use CauchyMatrix to compute the coefficients for an interpolating rational function with fixed poles:
Construct the rational function:
Visualize the interpolant in the complex plane:
Check that the rational interpolant does pass through all the given points:
Define the Parter matrix as a CauchyMatrix:
The Parter matrix is both a Cauchy matrix and a Toeplitz matrix:
The Parter matrix's dominant singular values are clustered around ![]() :
:
Properties & Relations (2)
Possible Issues (3)
The literature sometimes uses a different definition of the Cauchy matrix, where the second generating vector is negated:
If any of the generating vectors have repeated entries, a Cauchy matrix cannot be constructed:
If a component of any one of the generating vectors is the negative of a component of the other generating vector, a Cauchy matrix cannot be constructed:
Related Guides
Text
Wolfram Research (2022), CauchyMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/CauchyMatrix.html (updated 2024).
CMS
Wolfram Language. 2022. "CauchyMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/CauchyMatrix.html.
APA
Wolfram Language. (2022). CauchyMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CauchyMatrix.html
BibTeX
@misc{reference.wolfram_2025_cauchymatrix, author="Wolfram Research", title="{CauchyMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CauchyMatrix.html}", note=[Accessed: 15-September-2025]}
BibLaTeX
@online{reference.wolfram_2025_cauchymatrix, organization={Wolfram Research}, title={CauchyMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/CauchyMatrix.html}, note=[Accessed: 15-September-2025]}