FourierDSTMatrix

FourierDSTMatrix[n]

2型の n×n 離散正弦変換行列を返す．

FourierDSTMatrix[n,m]

m 型の n×n 離散正弦変換行列を返す．

詳細とオプション

  • m 型の離散正弦変換行列の各項 Frsは以下で計算できる．
  • 1.DST-I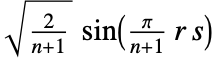
    2.DST-II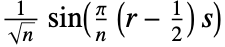
    3.DST-III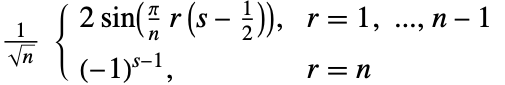
    4.DST-IV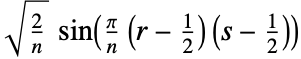
  • 1型，2型，3型，4型の離散正弦変換行列にはそれぞれ1型，2型，3型，4型の逆行列がある． »
  • FourierDSTMatrixの行は離散正弦変換の基底数列である．
  • FourierDSTMatrix[n].list の結果は，list の長さが n の場合は，FourierDST[list]と等価である．しかし，FourierDST[list]の計算の方がはるかに速く，数値誤差が小さい． »
  • 1型と4型については，返す行列の構造を指定するオプションTargetStructureがサポートされている．次は，TargetStructureの可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Hermitian"行列をエルミート行列として表す
    "Orthogonal"行列を直交行列として表す
    "Symmetric"行列を対称行列として表す
    "Unitary"行列をユニタリ行列として表す
  • FourierDSTMatrix[…,TargetStructureAutomatic]はFourierDSTMatrix[…,TargetStructure"Dense"]に等しい．
  • FourierDSTMatrix[…,WorkingPrecision->p]は精度が p である項目の行列を与える．

例題

すべて開くすべて閉じる

例  (1)

4×4離散正弦変換行列：

スコープ  (1)

離散正弦変換の長さ128の基底数列：

オプション  (2)

TargetStructure  (1)

離散正弦変換行列を密な行列として返す：

離散正弦変換行列を直交行列として返す：

離散正弦変換行列を対称行列として返す：

WorkingPrecision  (1)

機械精度を使う：

任意精度を使う：

アプリケーション  (1)

三重対角テプリッツ(Toeplitz)行列：

その固有ベクトルの行列は1型の離散正弦変換行列の対角リスケーリングとして表すことができる：

三重対角行列を対角化する：

特性と関係  (2)

離散正弦変換行列にベクトルを掛けることはそのベクトルの離散正弦変換を計算することと等価である：

FourierDSTは行列に基づいた計算よりもはるかに速い：

1型の離散正弦変換行列はそれ自身の逆行列である：

3型の離散正弦変換は2型の行列の逆行列である：

4型の離散正弦変換行列はそれ自身の逆行列である：

Wolfram Research (2012), FourierDSTMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierDSTMatrix.html （2024年に更新）.

テキスト

Wolfram Research (2012), FourierDSTMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierDSTMatrix.html （2024年に更新）.

CMS

Wolfram Language. 2012. "FourierDSTMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FourierDSTMatrix.html.

APA

Wolfram Language. (2012). FourierDSTMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDSTMatrix.html

BibTeX

@misc{reference.wolfram_2024_fourierdstmatrix, author="Wolfram Research", title="{FourierDSTMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDSTMatrix.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourierdstmatrix, organization={Wolfram Research}, title={FourierDSTMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/FourierDSTMatrix.html}, note=[Accessed: 14-November-2024 ]}