FourierDCTMatrix

FourierDCTMatrix[n]

returns an n×n discrete cosine transform matrix of type 2.

FourierDCTMatrix[n,m]

returns an n×n discrete cosine transform matrix of type m.

Details and Options

  • Each entry Frs of the discrete cosine transform matrix of type m is computed as:
  • 1.DCT-I
    2.DCT-II
    3.DCT-III
    4.DCT-IV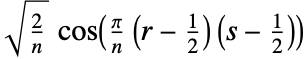
  • The discrete cosine transform matrices of types 1, 2, 3 and 4 have inverses of type 1, 3, 2 and 4, respectively. »
  • Rows of the FourierDCTMatrix are basis sequences of the discrete cosine transform.
  • The result of FourierDCTMatrix[n].list is equivalent to FourierDCT[list] when list has length n. However, the computation of FourierDCT[list] is much faster and has less numerical error. »
  • For type 4, the option TargetStructure is supported, which specifies the structure of the returned matrix. Possible settings for TargetStructure include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Hermitian"represent the matrix as a Hermitian matrix
    "Orthogonal"represent the matrix as an orthogonal matrix
    "Symmetric"represent the matrix as a symmetric matrix
    "Unitary"represent the matrix as a unitary matrix
  • FourierDCTMatrix[…,TargetStructureAutomatic] is equivalent to FourierDCTMatrix[…,TargetStructure"Dense"].
  • FourierDCTMatrix[…,WorkingPrecision->p] gives a matrix with entries of precision p.

Examples

open allclose all

Basic Examples  (1)

A 4×4 DCT matrix:

Scope  (1)

The discrete cosine transform's basis sequences of length 128:

Options  (2)

TargetStructure  (1)

Return the DCT matrix as a dense matrix:

Return the DCT matrix as an orthogonal matrix:

Return the DCT matrix as a symmetric matrix:

WorkingPrecision  (1)

Use machine precision:

Use arbitrary precision:

Applications  (1)

Define 2D discrete cosine transform of size 8×8 using matrix formulation:

Simplified JPEG compression algorithm:

Compare the original and compressed images:

Properties & Relations  (2)

A DCT matrix multiplied by a vector is equivalent to the discrete cosine transform of that vector:

FourierDCT is much faster than the matrix-based computation:

A discrete cosine transform matrix of type 1 is its own inverse:

A discrete cosine transform matrix of type 3 is an inverse of the type 2 matrix:

A discrete cosine transform matrix of type 4 is its own inverse:

Wolfram Research (2012), FourierDCTMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCTMatrix.html (updated 2024).

Text

Wolfram Research (2012), FourierDCTMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDCTMatrix.html (updated 2024).

CMS

Wolfram Language. 2012. "FourierDCTMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FourierDCTMatrix.html.

APA

Wolfram Language. (2012). FourierDCTMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDCTMatrix.html

BibTeX

@misc{reference.wolfram_2025_fourierdctmatrix, author="Wolfram Research", title="{FourierDCTMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDCTMatrix.html}", note=[Accessed: 29-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fourierdctmatrix, organization={Wolfram Research}, title={FourierDCTMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/FourierDCTMatrix.html}, note=[Accessed: 29-May-2025 ]}