Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

ThreeJSymbol

ThreeJSymbol

ThreeJSymbol[{j₁,m₁},{j₂,m₂},{j₃,m₃}]

gives the values of the Wigner 3‐ symbol.

Details

The 3‐ symbols vanish except when and the satisfy a triangle inequality.
The parameters of ThreeJSymbol can be integers, half‐integers or symbolic expressions.
The 3‐ symbols and Clebsch–Gordan coefficients in the Wolfram Language satisfy the relation .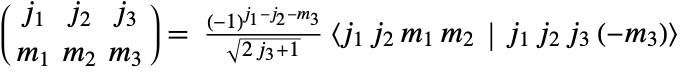

Examples

open all close all

Basic Examples (2)

Evaluate a 3‐ symbol with integer arguments:

Use symbolic arguments to obtain exact symbolic answers:

Scope (2)

ThreeJSymbol works with integer and half‐integer arguments:

TraditionalForm formatting:

Applications (3)

Plot 3‐ symbol coefficients as a function of and :

Apply angular momentum operators to spherical harmonics:

Evaluate Gaunt coefficients:

Evaluate as an explicit triple integral of spherical harmonics:

Properties & Relations (4)

Evaluate the completely symbolic case of ThreeJSymbol:

Demonstrate ‐sum orthogonality:

Convert a 3‐ symbol to a Regge R symbol:

Check the symmetry of the Regge R symbol:

Compare with the sum definition:

Possible Issues (1)

A message is issued and the result 0 returned in the case :

Top