VandermondeMatrix

VandermondeMatrix[{x1,x2,…,xn}]

ノード xiに対応する n×n Vandermonde行列を与える．

VandermondeMatrix[{x1,x2,…,xn},k]

n×k Vandermonde行列を与える．

VandermondeMatrix[vmat]

Vandermonde行列 vmat を構造化配列に変換する．

詳細とオプション

  • Vandermonde行列は，構造化配列として表された場合は，Det，Inverse，LinearSolve等の効率的な格納とより効率的な操作を可能にする．
  • Vandermonde行列は多項式補間に関係する計算および単項式基底におけるモーメントの計算に出現する．
  • ノード xiは数値である必要はなく，すべてが異なっていなくてもよい．
  • 合流型ではないVandermonde行列（xiは異なる）の成分は 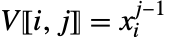で与えられる．
  • 合流型のVandermonde行列（xiがすべて異なる訳ではない）は，2つあるいはそれ以上のノードが互いに近付くことができるのであれば非合流型Vandermonde行列の制限された形である． »
  • 非合流型の場合，解{a0,…}=LinearSolve[V,{b1,…}]は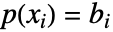，となるように点{xi,bi}を補関する多項式 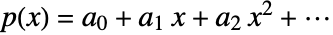の係数を与える．
  • 合流型の場合，解{a0,…}=LinearSolve[V,{b1,…}]はエルミート補間多項式の係数を与える．ただし，繰り返される xiは与えられる派生情報に相当する．
  • VandermondeMatrixについて加速される操作には以下がある．
  • Dettime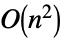
    Inversetime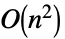
    LinearSolvetime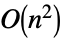
  • VandermondeMatrix sa については，sa["prop"]で次の特性"prop"にアクセスすることができる．
  • "Nodes"ノード xiのベクトル
    "Multiplicities"一意的な各ノードの多重度
    "Permutation"置換リスト
    "Confluent"行列が合流型かどうか
    "Transposed"行列が転置されているかどうか
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列によって格納された内部データ
    "StructuredAlgorithms"構造化配列に対して特別なメソッドを持つ関数のリスト
    "Summary"Datasetとして表される情報の要約
  • Normal[VandermondeMatrix[x]]はVandermonde行列を通常の行列として与える．
  • VandermondeMatrix[…,TargetStructure->struct]は，Vandermonde行列を struct で指定された形式で返す．次はその可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Structured"行列を構造化配列として表す
  • VandermondeMatrix[…,TargetStructureAutomatic]はVandermondeMatrix[…,TargetStructure"Structured"]に等しい．

例題

すべて開くすべて閉じる

例  (2)

Vandermonde行列を記号成分で構築する：

要素を表示する：

行列式を取得する：

Vandermonde行列を数値成分で構築する：

行列の通常表現を取得する：

線形系を行列で解く（双対Vandermonde問題）：

解は余弦を近似する補間多項式の係数を与える：

スコープ  (8)

矩形Vandermonde行列：

要素を表示する：

合流型Vandermonde行列：

要素を表示する：

矩形合流型Vandermonde行列：

要素を表示する：

非合流型Vandermonde行列を構造化配列として表す：

要素を表示する：

構造化表現は，通常，メモリ使用量がはるかに少ない：

VandermondeMatrixオブジェクトは配列についての情報を与える特性を含んでいる：

"Nodes"特性は，Vandermonde行列を生成するノードのベクトルを与える：

"Permutation"特性は，Vandermonde行列に関連付けられた置換ベクトルを与える：

"Multiplicities"特性は，一意的な各ノードの多重度を与える：

"Confluent"特性は，Vandermonde行列が合流型のときはTrueを，それ以外のときはFalseを与える：

"Transposed"特性はVandermonde行列が転置されているときはTrueを，それ以外の場合はFalseを与える：

"Summary"特性は，配列についての情報の簡単な要約を与える：

"StructuredAlgorithms"特性は，表現の構造を使うアルゴリズムを有する関数のリストを与える：

構造化アルゴリズムは，一般に，より高速でより正確である：

厳密な行列式が計算できる：

VandermondeMatrixから計算された値ははるかに正確である：

構造化アルゴリズムは悪条件から問題を遠ざけることがある：

VandermondeMatrixを使って線形系 を解く：

通常の行列を使って線形系を解く：

剰余はVandermondeMatrixを使った方が小さい：

構造化アルゴリズムは，適切な場合は別の構造化アルゴリズムを返す：

その共役転置を評価すると構造化された結果が与えられる：

もとの行列との積はもはやVandermonde行列ではない：

オプション  (1)

TargetStructure  (1)

Vandermonde行列を密な行列として返す：

Vandermonde行列を構造化配列として返す：

アプリケーション  (7)

n+1例の異なるサンプルの集合を関数から生成する：

VandermondeMatrixを使ってそれらのサンプルにおける関数を補間する次数 n の多項式を求める：

多項式を定義する：

もとの関数と補間多項式を比較する：

補間条件 と導関数の条件 を満足する多項式 の係数を定義する：

多項式を定義する：

補間条件と導関数の条件が満足されていることを確認する：

異なる4つの点の集合を定義する：

二次Vandermonde多項式をこれらの点にフィットする：

VandermondeMatrixの逆行列の列は，ラグランジュ(Lagrange)多項式と呼ばれる次数 n の多項式 の集合を定義する：

ラグランジュ多項式は恒等式 L_i(x_j)=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]を満足する：

Vandermonde多項式をラグランジュ多項式によって表す：

プロットして確かめる：

根を持つ多項式を定義する：

VandermondeMatrixを根から構築する：

既知の根がある多項式のフロベニウス(Frobenius)同伴行列はこの根を持つ対角行列と相似であり，Vandermonde行列が相似変換として機能する：

フロべニウス同伴行列の最終列には n-1次数までの多項式の負の係数が含まれている：

これらは初等対称多項式とも符号まで等しい：

n 次有限差分の係数について解く：

有限差分式を組み立てる：

これはDifferenceQuotientの結果に等しい：

閉じたニュートン・コーツ(Newton–Cotes)の公式のノードと重みを計算する関数を定義する[MathWorld]：

台形規則は次数1のニュートン・コーツの公式である：

シンプソンの公式は次数2のニュートン・コーツの公式である：

ブールの公式は次数4のニュートン・コーツの公式である：

指数関数の n 項の和：

点で指数関数のサンプルを取る：

Pronyのメソッド[Wikipedia]を使って指数関数の和をデータから復元する：

特性と関係  (6)

合流型Vandermonde行列は，非合流型行列の極限として得ることができる：

各行の連続する差分商を取る：

のときの極限は合流型Vandermonde行列である：

FourierMatrixはVandermondeMatrixとして表すことができる：

多項式の行列式はVandermondeMatrixのDet の平方として表すことができる：

合流型Vandermonde系を解く：

これは，微分値を指定したInterpolatingPolynomialの係数である：

対角行列，Vandermonde行列，ハンケル(Hankel)行列によって，Vandermonde行列の逆行列の因数分解を行う：

コーシー行列を対角行列，Vandermonde行列，ハンケル行列の積として表す：

おもしろい例題  (2)

行列とベクトル：

与えられた行列とベクトルからKrylov行列を計算する関数を定義する：

行列の固有値を計算する：

ベクトルに対する指数行列の動作はKrylov行列とVandermonde行列の逆行列によって表すことができる：

MatrixExpからも同じ結果が得られることを確認する：

DSolveValueからも同じ結果が得られることを確認する：

線形Caputo微分方程式もまた，Mittag–Leffler関数MittagLefflerEとともに，Krylov行列とVandermonde行列の逆行列によって解くことができる：

DSolveValueで同じ結果が得られることを確認する：

陰的ルンゲ・クッタ(Runge–Kutta)法のブッチャー(Butcher)配列は，ルジャンドル(Legendre)多項式の根から構築された主Vandermonde系を解くことで得られる：

陰的ルンゲ・クッタ・ガウス係数を指定精度で計算する関数を定義する：

NDSolveValueの係数を使ってShampine法による火炎伝播をモデル化する硬い微分方程式を解く：

厳密解の結果と比較する：

Wolfram Research (2022), VandermondeMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/VandermondeMatrix.html （2023年に更新）.

テキスト

Wolfram Research (2022), VandermondeMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/VandermondeMatrix.html （2023年に更新）.

CMS

Wolfram Language. 2022. "VandermondeMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/VandermondeMatrix.html.

APA

Wolfram Language. (2022). VandermondeMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VandermondeMatrix.html

BibTeX

@misc{reference.wolfram_2024_vandermondematrix, author="Wolfram Research", title="{VandermondeMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/VandermondeMatrix.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vandermondematrix, organization={Wolfram Research}, title={VandermondeMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/VandermondeMatrix.html}, note=[Accessed: 14-November-2024 ]}