VandermondeMatrix

VandermondeMatrix[{x1,x2,…,xn}]

给出与节点 xi 相对应的 n×n Vandermonde 矩阵.

VandermondeMatrix[{x1,x2,…,xn},k]

给出 n×k Vandermonde 矩阵.

VandermondeMatrix[vmat]

将 Vandermonde 矩阵 vmat 转换为结构化数组.

更多信息和选项

  • 当表示为结构化数组时，Vandermonde 矩阵可进行更高效的存储和更高效的运算，包括 Det、Inverse 和 LinearSolve.
  • Vandermonde 矩阵出现在与多项式插值相关的计算以及单项式基的矩计算中.
  • 节点 xi 不必是数字，也不必是不同的.
  • 非合流 Vandermonde 矩阵（不同的 xi）中的元素由 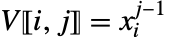给出.
  • 当允许两个或多个节点相互接近时，合流 Vandermonde 矩阵（不是所有的 xi 都相异）是非合流 Vandermonde 矩阵极限形式. »
  • 对于非合流 Vandermonde 矩阵，解 {a0,…}=LinearSolve[V,{b1,…}] 给出多项式 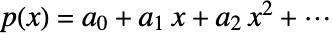的系数，对点 {xi,bi} 进行插值，使得 .
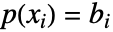  • 对于合流 Vandermonde 矩阵，解 {a0,…}=LinearSolve[V,{b1,…}] 给出 Hermite 插值多项式的系数，其中重复的 xi 对应于所提供的导数信息.
  • VandermondeMatrix 可以加快运算速度的计算包括：
  • Det用时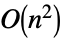
    Inverse用时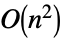
    LinearSolve用时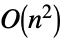
  • 对于 VandermondeMatrix sa，可通过 sa["prop"] 访问以下属性 "prop"：
  • "Nodes"节点 xi 组成的向量
    "Multiplicities"每个唯一节点的重数
    "Permutation"置换列表
    "Confluent"矩阵是否是合流的
    "Transposed"矩阵是否被转置
    "Properties"支持的属性列表
    "Structure"结构化数组的类型
    "StructuredData"结构化数组保存的内部数据
    "StructuredAlgorithms"可对结构化数组使用特殊方法的函数的列表
    "Summary"汇总信息，用 Dataset 表示
  • Normal[VandermondeMatrix[x]] 以普通矩阵的方式给出 Vandermonde 矩阵.
  • VandermondeMatrix[…,TargetStructure->struct] 以 struct 指定的格式返回 Vandermonde 矩阵. 可能的设置包括：
  • Automatic自动选择返回的表示
    "Dense"将矩阵表示为稠密矩阵
    "Structured"将矩阵表示为结构化数组
  • VandermondeMatrix[…,TargetStructureAutomatic] 等价于 VandermondeMatrix[…,TargetStructure"Structured"].

范例

打开所有单元关闭所有单元

基本范例  (2)

用符号元素构建 Vandermonde 矩阵：

显示元素：

获取行列式：

构造一个含有数值元素的 Vandermonde 矩阵：

获取矩阵的普通表示：

用矩阵求解线性方程组（对偶 Vandermonde 问题）：

解给出了对余弦进行近似的插值多项式的系数：

范围  (8)

矩形 Vandermonde 矩阵：

显示元素：

合流 Vandermonde 矩阵：

显示元素：

矩形合流 Vandermonde 矩阵：

显示元素：

将非合流 Vandermonde 矩阵表示为结构化数组：

显示元素：

结构化表示通常使用更少的内存：

VandermondeMatrix 对象包含可提供数组信息的属性：

"Nodes" 属性给出生成 Vandermonde 矩阵的节点向量：

"Permutation" 属性给出与 Vandermonde 矩阵关联的置换向量：

"Multiplicities" 属性给出每个唯一节点的重数：

如果 Vandermonde 矩阵是合流矩阵，"Confluent" 属性给出 True，否则给出 False：

如果 Vandermonde 矩阵被转置，"Transposed" 属性给出 True，否则给出 False：

"Summary" 属性给出了有关数组信息的简明总结：

"StructuredAlgorithms" 属性给出了一个函数列表，这些函数含有针对结构化表示的算法：

结构化算法通常更快和/或更准确：

可对行列式进行精确计算：

VandermondeMatrix 算出的值要准确得多：

结构化算法可以避免因病态条件出现问题：

用 VandermondeMatrix 求解线性方程组 ：

用普通矩阵求解线性方程组：

用 VandermondeMatrix 得到的残差更小：

合适的情况下，结构化算法会返回另一个结构化数组：

计算矩阵的共轭转置给出结构化结果：

与原始矩阵的乘积不再是 Vandermonde 矩阵：

选项  (1)

TargetStructure  (1)

将 Vandermonde 矩阵作为稠密矩阵返回：

将 Vandermonde 矩阵作为结构化数组返回：

应用  (7)

根据函数生成 n+1 不同的样本：

用 VandermondeMatrix 求 n 次多项式，在这些样本处对函数进行插值：

定义多项式：

将原始函数与插值多项式进行比较：

确定满足插值条件 和导数条件 的的多项式 的系数：

定义多项式：

验证是否满足插值和导数条件：

定义 4 个不同的点：

将三次 Vandermonde 多项式拟合到点集：

VandermondeMatrix 的逆矩阵的列定义了一组 n 次多项式 ，被称为拉格朗日多项式：

拉格朗日多项式满足恒等式 L_i(x_j)=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]：

用拉格朗日多项式表示 Vandermonde 多项式：

绘图并进行对比：

定义一个根为 的多项式：

根据根构建 VandermondeMatrix：

具有已知根的多项式的 Frobenius 伴随矩阵类似于包含根的对角矩阵，其中 Vandermonde 矩阵相当于相似变换：

Frobenius 伴随矩阵的最后一列包含多项式的系数的负值，最高为 n-1 次项：

对基本对称多项式也一样，只是正负号不同：

求 n 阶有限差分式的系数：

组合有限差分式：

与 DifferenceQuotient 的结果等价：

定义一个函数来计算闭合牛顿-柯特斯法则 [MathWorld] 的节点和权重：

梯形规则是 1 阶牛顿-科特斯公式：

辛普森规则是 2 阶牛顿-科特斯公式：

布尔规则是 4 阶牛顿-科特斯公式：

指数函数的 n 项和：

在 个点上对指数函数进行采样：

用 Prony's method [Wikipedia] 从数据中恢复指数和：

属性和关系  (6)

可以通过非合流矩阵的极限获取合流 Vandermonde 矩阵：

取每一行的连续差商：

时的极限即为合流 Vandermonde 矩阵：

FourierMatrix 可被表示为 VandermondeMatrix：

多项式的判别式可被表示为 VandermondeMatrix 的 Det 的平方：

求解合流 Vandermonde 系统：

以下是导数值已指定条件下的 InterpolatingPolynomial 的系数：

演示用对角矩阵、Vandermonde 和 Hankel 矩阵进行 Vandermonde 矩阵的逆矩阵的因式分解：

将 Cauchy 矩阵表示为对角矩阵、Vandermonde 和 Hankel 矩阵的乘积：

巧妙范例  (2)

矩阵和向量：

定义一个函数，用于根据给定的矩阵和向量计算 Krylov 矩阵：

计算矩阵的特征值：

矩阵指数对向量的作用可以用 Krylov 矩阵和 Vandermonde 矩阵的逆矩阵表示：

验证可以用 MatrixExp 获得相同的结果：

验证可以用 DSolveValue 获得相同的结果：

线性 Caputo 微分方程也可以用 Krylov 矩阵和 Vandermonde 矩阵的逆矩阵以及 Mittag–Leffler 函数 MittagLefflerE 求解：

验证可以用 DSolveValue 获得相同的结果：

隐式 Runge-Kutta 方法的 Butcher 表可以通过求解根据 Legendre 多项式的根构造的原始 Vandermonde 方程组来获得：

定义一个函数来计算给定精度的隐式龙格-库塔-高斯系数：

在 NDSolveValue 中使用这些系数来求解刚性微分方程，模拟由于 Shampine 引起的火焰传播：

将结果与精确解相比较：

Wolfram Research (2022)，VandermondeMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VandermondeMatrix.html （更新于 2023 年）.

文本

Wolfram Research (2022)，VandermondeMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/VandermondeMatrix.html （更新于 2023 年）.

CMS

Wolfram 语言. 2022. "VandermondeMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/VandermondeMatrix.html.

APA

Wolfram 语言. (2022). VandermondeMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/VandermondeMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_vandermondematrix, author="Wolfram Research", title="{VandermondeMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/VandermondeMatrix.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vandermondematrix, organization={Wolfram Research}, title={VandermondeMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/VandermondeMatrix.html}, note=[Accessed: 14-November-2024 ]}