



ToGradedMesh
Details and Options
- A graded mesh is a nonuniform or anisotropic mesh where the spacing between coordinates varies exponentially.
- A graded mesh is used to capture steep gradients or discontinuities in partial differential equations or their boundaries.
- The following optional properties prop can be given:
-
"Alignment"adir "Uniform" use alignment direction adir "ElementCount"n Automatic use n elements "ElementMarker"m 0 use ElementMarker m "GradingRatio"r Automatic use grading ratio r "MaximalDistance"dmax Automatic choose coordinates so that the maximal distance between coordinates is dmax "MinimalDistance"dmin Automatic choose coordinates so that the minimum distance between coordinates is dmin - The following alignments adir can be given:
-
"Left" high coordinate concentration on the left "Right" high coordinate concentration on the right "BothEnds" high coordinate concentration at both ends "Central" high coordinate concentration in the center "Uniform" use uniform spacing between coordinates fun[interval,props] use the function fun for interval interval and properties props - ToGradedMesh accepts a 1D Line primitive and returns a graded 1D ElementMesh.
- The default minimal distance between the element end coordinates is computed as
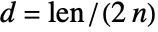 , where
, where 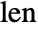 is the distance between the endpoints of the input Line element and
is the distance between the endpoints of the input Line element and 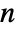 is the element count.
is the element count. - ToGradedMesh has the following options:
-
"MeshOrder" Automatic order of the element mesh
Examples
open all close allBasic Examples (3)
Create a uniform mesh for the interval ![]() :
:
Create a graded mesh with a high coordinate concentration on the left:
Convert the Line to a graded mesh with a "BothEnds" point distribution using default values:
Scope (25)
Basic Usage (5)
Convert the Line from –1 to 1 to a graded mesh with a "Right" point distribution:
Convert the Line from –1 to 1 to a graded mesh with a "Central" point distribution:
Convert the Line from –1 to 1 to a graded mesh with a "Left" point distribution:
Convert the Line from –1 to 1 to a graded mesh with a "Left" point distribution:
Alignment (3)
Make a uniform 1D mesh on the unit interval:
Convert the Line to a graded mesh with a "Central" point distribution, 10 elements and a minimal coordinate distance of ![]() :
:
Compute the minimal distance between the coordinates:
Specify a function to give a mesh with Chebyshev node spacing:
ElementCount (3)
Make a uniform 1D mesh on the unit interval using 47 elements:
Convert the Line to a graded mesh having more points on the right and creating 50 elements:
Convert the Line from –1 to 1 to a graded mesh with a "Central" point distribution using default values:
The number of default elements is 20. This produces the same mesh:
MaximalDistance (1)
MinimalDistance (4)
Convert the Line to a graded mesh having more points on the right, where the initial spacing is 1/50:
Find the minimal distance used:
Make a uniform 1D mesh on the unit interval using a distance of 0.025 between points:
Find the minimal distance used:
Convert the Line to a graded mesh with a "Central" point distribution:
Compute the minimal distance between the adjacent coordinates:
At the central points, the distance between the adjacent first-order coordinates is computed by dividing the length of the region by two times the number of elements: ![]() .
.
This constructs the same mesh:
Compute the minimal distance between the adjacent coordinates:
Convert the Line to a graded mesh having more points on the left and creating 10 elements, where the minimal spacing is 1/33:
Compute the minimal distance between the adjacent coordinates:
GradingRatio (4)
Convert the Line to a graded mesh with a "Central" point distribution and a grading ratio ![]() :
:
Convert the Line to a graded mesh having more points on the right and creating 10 elements, where the grading ratio is ![]() :
:
Convert the Line to a graded mesh having more points on the right, where the grading ratio is ![]() :
:
Compute the distance between the adjacent coordinates:
Note the growth factor is two.
Convert the Line to a graded mesh having more points at the ends, where the grading ratio is ![]() :
:
Compute the distance between the adjacent coordinates:
Note that the length of the elements from the ends to the center grows with a factor of 2.
Multi-material Regions (5)
Create a right-, both ends– and left-aligned mesh from three line primitives:
Create a left-aligned mesh with a maximal distance that is connected to a uniform mesh with the same maximal distance:
Create the same mesh with an element marker in the different sections:
Extract the union of the element markers:
Convert three Line primitives to a graded mesh, assigning a mesh coordinate distribution to each line and three region markers: ![]() :
:
Visualize the mesh coordinate distribution and the markers:
Convert three Line primitives to a graded mesh, assigning a mesh coordinate distribution and an element region marker to each line:
Options (4)
"MeshOrder" (4)
Create a graded mesh with a high coordinate concentration on the left:
Create a first-order mesh with a high coordinate concentration on the left:
Create a graded first-order mesh with a high coordinate concentration on the right:
Using a log scale, visualize how the nodes are distributed along the anisotropic mesh:
Create a second-order graded mesh with a high coordinate concentration on the left:
Using a log scale, visualize how the second-order nodes are distributed along the graded mesh:
The mesh data structure stores the second-order nodes after the first-order nodes. Using a log scale, visualize how the sorted second-order nodes are distributed along the graded mesh:
Applications (4)
Create a 2D graded mesh from a product of two 1D graded meshes:
Create a 1D graded mesh with a "Central" point distribution:
Create a second 1D graded mesh with a "Central" point distribution and 50 elements:
Visualize the region product of the anisotropic mesh:
Create a third 1D graded mesh with a "BothEnds" point distribution, 50 elements and an endpoint distance of 1/200:
Solve the following system of diffusion equations over the domain of ![]() :
:
With initial conditions ![]() and
and ![]() and boundary conditions at
and boundary conditions at ![]() ,
, ![]() and
and ![]() . At
. At ![]() ,
, ![]() and
and ![]() .
.
To model the infinite domain, create a left-aligned graded mesh over the Line segments from ![]() with 150 elements and a minimal distance of 1/1000:
with 150 elements and a minimal distance of 1/1000:
This mesh allows you to have a fine mesh resolution on the left and only few elements on the right, just to extend the domain far enough to mimic an infinite domain without needing an excessive amount of mesh elements and thus unnecessarily increasing computation time.
Set up the variables and parameters where ![]() and
and ![]() :
:
Set up the PDE with initial conditions ![]() :
:
For comparison, solve the PDE just over the domain ![]() :
:
Visualize the solution in the domain ![]() for time
for time ![]() :
:
Note that the extension to a larger domain is necessary to capture the behavior of the boundary condition at infinity.
Over the unit square domain, solve an orthotropic diffusion equation ![]() with a large difference in scale of the diffusion coefficient. A constant Dirichlet boundary condition is given on the left and a discontinuous Dirichlet boundary condition is given on the right boundary. Define the PDE:
with a large difference in scale of the diffusion coefficient. A constant Dirichlet boundary condition is given on the left and a discontinuous Dirichlet boundary condition is given on the right boundary. Define the PDE:
Due to the large difference in scale of the diffusion coefficient in the ![]() direction, the PDE is essentially one-dimensional in the
direction, the PDE is essentially one-dimensional in the ![]() direction. To deal with the discontinuity of the Dirichlet condition at
direction. To deal with the discontinuity of the Dirichlet condition at ![]() and
and ![]() , a graded mesh is constructed.
, a graded mesh is constructed.
Create a 1D mesh with 10 elements:
Create a graded mesh with "Central" alignment and 50 elements in each:
Visualize the region product of the anisotropic mesh:
Visualize the density plot of the result:
Visualize the derivative of ϕ in the x direction at x=1:
To assess the quality of the solutions, it is instructive to compare the solution with a graded mesh to a default mesh solution:
Note that the function behavior has less overshoot with the anisotropic mesh:
Note that the anisotropic mesh solution function derivative has more overshoot but in a smaller region.
Possible Issues (7)
With "Left" or "Right" alignment, the minimum number of elements is 1:
With "Central" or "BothEnds" alignment, the minimum value of ![]() , the number of elements, is 2:
, the number of elements, is 2:
A "Right" or "Left" point distribution cannot be created if the minimal distance ![]() with the length
with the length ![]() of the input Line and the element count
of the input Line and the element count ![]() :
:
Use a smaller minimal distance ![]() :
:
A "BothEnds" or "Central" point distribution cannot be created if the minimal distance ![]() with the length
with the length ![]() of the input Line and the element count
of the input Line and the element count ![]() :
:
Use a smaller minimal distance ![]() :
:
A ToGradedMesh cannot be created if the grading ratio is less than or equal to 0:
Use a positive grading ratio ![]() :
:
Mesh generation will not work as expected when the distance ![]() between the closest coordinates is greater than the distance between the endpoints of the input mesh over the number of elements.
between the closest coordinates is greater than the distance between the endpoints of the input mesh over the number of elements.
Consider an input Line with a distance between endpoints equal to 2 (![]() ). The input Line will be converted to a graded mesh with 5 elements (
). The input Line will be converted to a graded mesh with 5 elements (![]() ), a distance between closest coordinates equal to 1 (
), a distance between closest coordinates equal to 1 (![]() ) and a "Left" alignment:
) and a "Left" alignment:
Use a smaller minimal distance:
The property "GradingRatio" has no meaning for a uniform alignment:
Neat Examples (1)
Specify a function to describe a point distribution:
Create a graded mesh where the point distribution is given by a function:
Compare this to a function that uses Fibonacci numbers as a distribution. Write a function to get a Fibonacci distribution:
Convert the Line to a graded mesh using a function to specify the distribution of points:
Verify that distance between the elements follows a Fibonacci pattern:
Compare the two different distributions:
Using a log scale, visualize the node distribution in fibmesh and mesh:
Note that for the construction of the Fibonacci distribution it is not necessary to provide the initial spacing, because a Fibonacci sequence only needs the number of elements, while other distributions use a power law approach to achieve a more uniform grading with a specified minimal distance.
Tech Notes
Related Guides
Text
Wolfram Research (2021), ToGradedMesh, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html.
CMS
Wolfram Language. 2021. "ToGradedMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html.
APA
Wolfram Language. (2021). ToGradedMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html
BibTeX
@misc{reference.wolfram_2025_togradedmesh, author="Wolfram Research", title="{ToGradedMesh}", year="2021", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_togradedmesh, organization={Wolfram Research}, title={ToGradedMesh}, year={2021}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html}, note=[Accessed: 25-February-2026]}