ToGradedMesh
詳細とオプション
- グレーデッドメッシュは,座標間の間隔が指数関数的に変化する不均一または異方性のメッシュである.
- グレーデッドメッシュは,偏微分方程式またはその境界における急激な勾配または不連続性を捉えるために使われる.
- 以下の任意の特性 prop を使うことができる.
-
"Alignment"adir "Uniform" アラインメントの方向 adir を使う "ElementCount"n Automatic n 個の要素を使う "ElementMarker"m 0 ElementMarker m を使う "GradingRatio"r Automatic 段階付けの率 r を使う "MaximalDistance"dmax Automatic 座標間の最長距離が dmax となるように座標を選ぶ "MinimalDistance"dmin Automatic 座標間の最短距離が dmin となるように座標を選ぶ - 以下のアラインメント adir を与えることができる.
-
"Left" 左に座標が多く集中している "Right" 右に座標が多く集中している "BothEnds" 両端に座標が多く集中している "Central" 中央に座標が多く集中している "Uniform" 座標間に一様の間隔を使う fun[interval,props] 関数 fun を区間 interval と特性 props に使う - ToGradedMeshは,1DLineプリミティブを受け取り,1DのグレーデッドElementMeshを返す.
- 要素の端の座標間のデフォルト最短距離は,
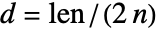 で計算される.ここで
で計算される.ここで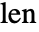 は入力のLine要素の端点間の距離,
は入力のLine要素の端点間の距離,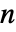 は要素数である.
は要素数である. - ToGradedMeshは以下のオプションを持つ.
-
"MeshOrder" Automatic 要素メッシュの次数
例題
すべて開くすべて閉じる例 (3)
Lineを,"BothEnds"の点分布でデフォルト値を使ったグレーデッドメッシュに変換する:
スコープ (26)
基本の用法 (5)
Alignment(アラインメント) (4)
ElementCount(要素数) (3)
MinimalDistance(最短距離) (4)
GradingRatio(段階付けの率) (4)
オプション (4)
アプリケーション (4)
2つの1Dのグレーデッドメッシュの積から,2Dのグレーデッドメッシュを作成する:
"Central"の点分布を持つ1Dのグレーデッドメッシュを作成する:
"Central"の点分布と50個の要素を持つ,2つ目の1Dのグレーデッドメッシュを作成する:
"BothEnds"の点分布と50個の要素を持ち,端点の距離が1/200である,3つ目の1Dのグレーデッドメッシュを作成する:
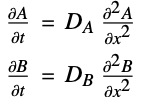
初期条件が ![]() および
および ![]() であり,
であり, ![]() における境界条件が
における境界条件が ![]() および
および ![]() である.
である.![]() において,
において,![]() および
および ![]() である.
である.
無限領域をモデル化するために,150個の要素と最短距離1/1000で,![]() からのLineの部分上で左揃えのグレーデッドメッシュを作成する:
からのLineの部分上で左揃えのグレーデッドメッシュを作成する:
このメッシュは,左に細かいメッシュの解像度,右に少しだけの要素を持ち,過剰な量のメッシュ要素を必要とすることなく,無限領域を模倣するのに十分な分だけ領域を拡張することができるので,不必要に計算時間を増やさずに済む.
無限大での境界条件の動作を捉えるためには,より大きな領域に拡張する必要がある.
単位正方領域上で,拡散係数のスケールに大きな違いがある直立異方性の拡散方程式 ![]() を解く.一定のディリクレ境界条件が左の境界に,不連続のディリクレ境界条件が右の境界に与えられる.偏微分方程式を定義する:
を解く.一定のディリクレ境界条件が左の境界に,不連続のディリクレ境界条件が右の境界に与えられる.偏微分方程式を定義する:
![]() 方向の拡散係数のスケールに大きな違いがあるため,偏微分方程式は基本的に
方向の拡散係数のスケールに大きな違いがあるため,偏微分方程式は基本的に ![]() 方向には一次元である.
方向には一次元である.![]() と
と ![]() におけるディリクレ条件の不連続性に対処するために,グレーデッドメッシュが構築される.
におけるディリクレ条件の不連続性に対処するために,グレーデッドメッシュが構築される.
"Central"のアラインメントでそれぞれ50個の要素を持つグレーデッドメッシュを作成する:
解の質を評価するために,グレーデッドメッシュの解とデフォルトのメッシュの解を比べると有益である:
考えられる問題 (7)
"Left"または"Right"のアラインメントでは,最小の要素数は1である:
"Central"または"BothEnds"のアラインメントでは,![]() の最小値,つまり要素数は2である:
の最小値,つまり要素数は2である:
"Right"または"Left"の点分布は,最短距離が![]() (入力Lineの長さが
(入力Lineの長さが![]() ,要素数が
,要素数が ![]() )の場合には作成できない:
)の場合には作成できない:
"BothEnds"または"Central"の点分布は,最短距離が ![]() (入力Lineの長さが
(入力Lineの長さが![]() ,要素数が
,要素数が ![]() )の場合には作成できない:
)の場合には作成できない:
ToGradedMeshは,段階付けの率が0以下である場合には作成できない:
メッシュ生成は,最も近い座標間の距離 ![]() が要素数上の入力メッシュの端点間の距離よりも長い場合には期待通りにいかない.
が要素数上の入力メッシュの端点間の距離よりも長い場合には期待通りにいかない.
端点間の距離が2(![]() )である入力の Lineについて考える.この入力Lineは,要素が5個(
)である入力の Lineについて考える.この入力Lineは,要素が5個(![]() )で,最も近い座標間の距離が1に等しく(
)で,最も近い座標間の距離が1に等しく(![]() ),"Left"のアライメントを持つグレーデッドメッシュに変換される:
),"Left"のアライメントを持つグレーデッドメッシュに変換される:
特性"GradingRatio"は,一様なアラインメントには意味を持たない:
おもしろい例題 (1)
点分布が関数によて与えられるグレーデッドメッシュを作成する:
これを,フィボナッチ数を分布として使う関数と比べる.フィボナッチ分布を得るための関数を書く:
点の分布を指定する関数を使って,Lineをグレーデッドメッシュに変換する:
要素間の距離がフィボナッチ数列のパターンに従うことを確かめる:
対数スケールを使って,fibmesh と mesh のノード分布を可視化する:
フィボナッチ分布の構築において,最初の間隔は必要ないことに注意する.他の分布は指定の最短距離を持つより一様な段階付けをベキ法則のアプローチを使うのに対し,フィボナッチ数列は要素の数のみが必要であるからである.
テキスト
Wolfram Research (2021), ToGradedMesh, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html.
CMS
Wolfram Language. 2021. "ToGradedMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html.
APA
Wolfram Language. (2021). ToGradedMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ToGradedMesh.html