HypothesisTesting`
HypothesisTesting`

MeanDifferenceTest

MeanDifferenceTest[list1,list2,Δμ0]

performs a test with null hypothesis μ1-μ2=Δμ0.

Details and Options

  • To use MeanDifferenceTest, you first need to load the Hypothesis Testing Package using Needs["HypothesisTesting`"].
  • MeanDifferenceTest[list1,list2, Δμ0] gives a 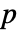‐value for the test that the difference between the means μ1 and μ2 of the populations from which list1 and list2 were sampled is significantly different from Δμ0.
  • MeanDifferenceTest is based on a normal distribution if the population variances are assumed known.
  • If the variances for the two populations are assumed equal and unknown, the test is based on Student's 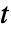distribution with Length[list1]+Length[list2]-2 degrees of freedom.
  • If the population variances are not assumed known and not assumed equal, Welch's approximation for the degrees of freedom is used.
  • The following options can be given:
  • EqualVariances Falsewhether the unknown population variances are assumed equal
    FullReport Falsewhether to include detailed information about a test
    KnownVariance Nonevariance of population
    SignificanceLevel Nonesignificance level of the test
    TwoSided Falsewhether to perform a two-sided test

Examples

open allclose all

Basic Examples  (1)

A test of the difference of population means against 0:

Options  (5)

EqualVariances  (1)

A test assuming equal variances:

FullReport  (1)

A full report for a mean difference test:

KnownVariance  (1)

A test assuming the population variances are 1 and 3:

SignificanceLevel  (1)

A test at significance level .01:

TwoSided  (1)

A two‐sided mean difference test:

Wolfram Research (2007), MeanDifferenceTest, Wolfram Language function, https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html.

Text

Wolfram Research (2007), MeanDifferenceTest, Wolfram Language function, https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html.

CMS

Wolfram Language. 2007. "MeanDifferenceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html.

APA

Wolfram Language. (2007). MeanDifferenceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html

BibTeX

@misc{reference.wolfram_2024_meandifferencetest, author="Wolfram Research", title="{MeanDifferenceTest}", year="2007", howpublished="\url{https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_meandifferencetest, organization={Wolfram Research}, title={MeanDifferenceTest}, year={2007}, url={https://reference.wolfram.com/language/HypothesisTesting/ref/MeanDifferenceTest.html}, note=[Accessed: 22-November-2024 ]}