IPOPTLink`
IPOPTLink`

IPOPTMinimize

IPOPTMinimize[f,{x1,…},{x1i0,…}]

numerically searches for a local minimum of f in xj, starting from the point xj=xj0.

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…}]

numerically searches for a local minimum subject to the variable bound constraints xj min≤xj≤xj max.

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…}]

numerically searches for a local minimum subject to function constraints gi min≤gi(x)≤gi max.

Details and Options

  • To use IPOPTMinimize, you first need to load it using Needs["IPOPTLink`"].
  • IPOPTMinimize numerically solves a real-valued minimization problem for an objective function 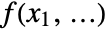subject to variable bound constraints and/or function constraints.
  • The objective f and the constraint functions {g1,…} should be real-valued and twice continuously differentiable.
  • The optimization problem need not be convex or linear.
  • Equality constraints 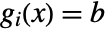may be specified by setting the constraint bounds to {b,b}. »
  • IPOPTMinimize returns a solution object in the form of an IPOPTData expression.
  • The following options can be given to IPOPTMinimize:
  • StepMonitor Noneexpression to evaluate whenever a step is taken
    IPOPTOptions {}options to be passed to the IPOPT library
    RuntimeOptions Automaticoptions to specify runtime settings
  • The IPOPT library options have string names and real, integer or string values.
  • Example options that can be specified in IPOPTOptions include:
  • "tol"realdesired convergence tolerance (relative)
    "max_iter"integermaximum number of iterations allowed
    "linear_solver"stringlinear solver to be used (e.g. "mumps")
  • The complete list of IPOPT library options and possible values can be found on the web page.

Examples

open allclose all

Basic Examples  (3)

Find a local minimum of starting from .

Extract the minimum value and position from the IPOPTData expression:

Plot the solution:

Minimize with variable bounds , , starting from .

Extract the minimum value and position from the IPOPTData expression:

Plot the solution:

Minimize with variable bounds , and function constraint , starting from .

Extract the minimum value and position from the IPOPTData expression:

Plot the solution:

Scope  (2)

Maximize a function by minimizing the negative of the objective value:

Find the maximum value and position from the IPOPTData expression:

Minimize a function with an equality constraint by specifying equal lower and upper bounds :

Extract the minimum value and position from the IPOPTData expression:

Options  (5)

StepMonitor  (1)

Steps taken by IPOPTMinimize in finding the minimum of a function:

IPOPTOptions  (2)

Use IPOPTOptions to set options as described in the IPOPT library documentation options page.

Use "tol" to set the relative error tolerance to 10.^-6:

With this option we can expect about 6 digits of precision:

Compare to the exact solution:

Use "max_iter" to set the maximum number of iterations to 5:

The error above indicates that the iterations were not enough to satisfy the default relative error tolerance of 10^-8:

RuntimeOptions  (2)

Use RuntimeOptions to specify runtime settings:

Use "RuntimeErrorHandler" to indicate whether to return an IPOPTData object or $Failed when a serious error occurs:

With some errors such as machine overflow, $Failed is returned with the Automatic setting:

Return a solution object so that the IPOPTReturnCode can be extracted:

Extract the return code:

Use "WarningMessges" to turn off and on the warning messages indicating runtime problems:

Turn off the warning messages:

Applications  (1)

Find the polygon with maximal area among polygons with sides and diameter . Let {r[i],t[i]} be the polar coordinates of the vertices of the polygon. The variables and their bounds are:

The area of the polygon is:

To state as a minimization problem negate the objective function:

Set up the constraints and the constraint bounds:

Define an initial point for the minimization:

Load the package and solve the minimization problem:

Extract the maximum area from the solution object:

Extract the optimal variable values from the solution object:

Find the points in Cartesian coordinates:

Plot the result:

Wolfram Research (2016), IPOPTMinimize, Wolfram Language function, https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

Text

Wolfram Research (2016), IPOPTMinimize, Wolfram Language function, https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

CMS

Wolfram Language. 2016. "IPOPTMinimize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

APA

Wolfram Language. (2016). IPOPTMinimize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html

BibTeX

@misc{reference.wolfram_2023_ipoptminimize, author="Wolfram Research", title="{IPOPTMinimize}", year="2016", howpublished="\url{https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html}", note=[Accessed: 26-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_ipoptminimize, organization={Wolfram Research}, title={IPOPTMinimize}, year={2016}, url={https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html}, note=[Accessed: 26-November-2024 ]}