Optimizing with IPOPT
| Unconstrained minimization | Maximizing with IPOPTMinimize |
| Bound constrained minimization | Engineering example |
| Function constrained minimization | References |
| ParametricIPOPTMinimize |
IPOPT (Interior Point OPTimizer) is a software package for large-scale nonlinear optimization, designed to find local solutions of mathematical optimization problems.
IPOPTLink is a Wolfram System application that uses Wolfram LibraryLink to link to IPOPT functions. IPOPTLink provides, among others, the functions IPOPTMinimize and ParametricIPOPTMinimize. These functions can be used for local minimization with or without parameters. They may be automatically called by optimization functions such as FindMinimum.
However, IPOPTLink functions can also be called directly providing a more flexible way to use the functionality implemented in IPOPT.
| IPOPTMinimize | compute local minimum using IPOPT |
| IPOPTData | data expression returned by IPOPTMinimize |
| IPOPTMinValue | gets the minimal objective value from IPOPTData expression |
| IPOPTArgMin | gets the local minimum position from IPOPTData expression |
| ParametricIPOPTMinimize | compute local minimum with parameters using IPOPT |
IPOPT is designed to find local solutions of mathematical constrained optimization problems in ![]() dimensions. Constrained optimization problems are problems for which a real valued function of several variables
dimensions. Constrained optimization problems are problems for which a real valued function of several variables ![]() , referred to as the objective function, is to be minimized subject to constraints. Two types of constraints may be specified -- either variable bound constraints or constraints defined by functions. Variable bound constraints are of the form
, referred to as the objective function, is to be minimized subject to constraints. Two types of constraints may be specified -- either variable bound constraints or constraints defined by functions. Variable bound constraints are of the form ![]() where x=(x1,…,xn). Function constraints are of the form
where x=(x1,…,xn). Function constraints are of the form ![]() .
.
Depending on the type of constraints IPOPTMinimize can be used in the following three ways :
| IPOPTMinimize[f(x),x,x0] | unconstrained minimization |
| IPOPTMinimize[f(x),x,x0,xbounds] | bound constrained minimization |
| IPOPTMinimize[f(x),x,x0,xbounds,g(x),gbounds] | constrained minimization by function constraints and variable bounds |
Maximizing an objective function can be done by minimizing the negative of the function to maximize.
Unconstrained minimization
| IPOPTMinimize[f,{x1,…},{x1i0,…}] | unconstrained minimization |
IPOPTMinimize unconstrained minimization.
In order to use IPOPTLink the package needs to be loaded.
As an initial example, find a local minimum of ![]() starting from
starting from ![]() .
.
Call the IPOPT solver using IPOPTMinimize with objective function ![]() , argument variables {
, argument variables {![]() } and initial value
} and initial value ![]() }.
}.
IPOPTMinimize returns an IPOPTData object. This object contains the minimal value.
The IPOPTData object also contains the coordinate point at which the minimum was found.
Bound constrained minimization
| IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…}] | bound constrained minimization |
IPOPTMinimize bound constrained minimization.
Find a local minimum of ![]() with x constrained in the interval
with x constrained in the interval ![]() , starting from
, starting from ![]() . We can again use IPOPTMinimize with objective function
. We can again use IPOPTMinimize with objective function ![]() , argument variable
, argument variable ![]() and initial value
and initial value ![]() . We also need to specify the variable bounds
. We also need to specify the variable bounds ![]() :
:
IPOPTMinimize returns an IPOPTData object. This object contains the minimal value and the minimization point.
Note that bound constraints are a special case of function constraints.
Function constrained minimization
| IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…}] | constrained minimization with function constraints and variable bounds |
IPOPTMinimize constrained minimization with function constraints and variable bounds.
Minimize ![]() over the circle
over the circle ![]() , described by a constraint function
, described by a constraint function![]() with lower and upper constraint bounds both equal to 1.
with lower and upper constraint bounds both equal to 1.
ParametricIPOPTMinimize
ParametricIPOPTMinimize can be used to set up a minimization problem with parameters present anywhere in the problem formulation. The optimization problem may then be solved repeatedly with different parameter values. ParametricIPOPTMinimize has all of the arguments of IPOPTMinimize with the addition of the parameter variables argument {p1,…} given last.
| ParametricIPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…},{p1,…}] | parametric constrained minimization |
ParametricIPOPTMinimize parametric constrained minimization.
Set up a minimization problem over the circle ![]() , where r is a parameter.
, where r is a parameter.
The previous step performs the preprocessing of the functions and all necessary derivatives and returns a ParametricFunction object awaiting parameter values.
The actual minimization begins after providing parameter values and the solution is stored in an IPOPTData expression.
Compute other solutions for different parameter values.
Using ParametricIPOPTMinimize instead of IPOPTMinimize with multiple parameter values reduces the overhead of repeatedly preprocessing the objective and constraint functions as well as all necessary derivatives, which can be significant depending on their complexity.
Maximizing with IPOPTMinimize
A maximum value can be found by minimizing the negative of the objective function.
Find a local maximum of ![]() over the circle
over the circle ![]() .
.
The minimum value of -f should then be negated again to obtain the maximum value of f.
Engineering example
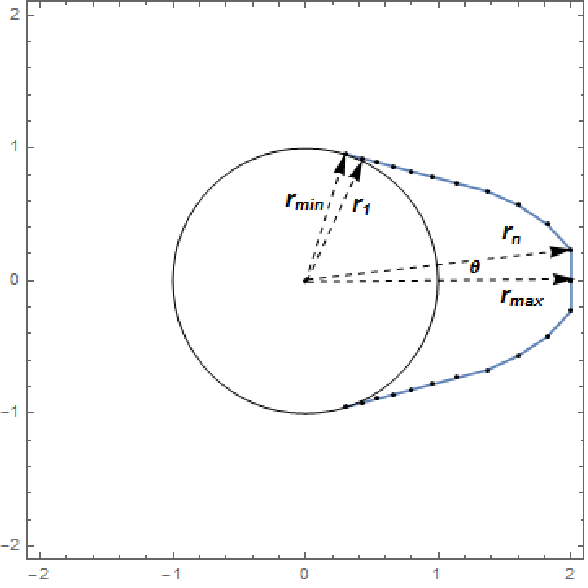
Design a cam to maximize the area of the valve opening for one rotation of the convex cam with constraints on the curvature and the radius of the cam. The problem formulation is from the COPS test suite and is summarized below.
We assume that the shape of the cam is circular over an angle of 6π/5 of its circumference with radius rmin. The design variables ri,i=1,…,n, represent the radius of the cam at equally spaced angles θ distributed over an angle of 2π/5. Symmetry is used in the remaining angle of 2π/5.
The following constraints are specified. Each radius ri is constrained in the interval {rmin, rmax}. Additionally we have convexity constraints expressed by A(ri-1,ri+1)≤A(ri-1,ri)+ A(ri,ri+1), where A(ri,rj) is the area of the triangle defined by the origin and the points ri and rj on the cam surface. There is also a curvature requirement -α ≤(ri+1-ri)/θ ≤α depending on the parameter α.
To define the objective function the valve opening area is assumed to have a simple linear relationship with the design variables ri given as: π rv 2(r1+…+rn)/n, where rv is a constant related to the geometry of the valve.
We can set this as a parametric problem with parameters rmin,rmax, α. The number of design variables is chosen to be n=20 and we assume ![]() .
.
References
IPOPT is written by Andreas Wächter, Carl Laird and others as part of the COIN-OR Initiative. It is based on the following paper: A. Wächter and L. T. Biegler, On the Implementation of a Primal-Dual Interior Point Filter Line Search Algorithm for Large-Scale Nonlinear Programming, Mathematical Programming 106(1), pp. 25-57, 2006.