WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

IPOPTMinimize[f,{x1,…},{x1i0,…}]

xj についての f の極小値をxj=xj0 から始めて数値的に検索する．

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…}]

変数境界制約条件 xj min≤xj≤xj max の下で極小値を数値的に検索する．

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…}]

関数制約条件 gi min≤gi(x)≤gi max の下で極小値を数値的に検索する

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
StepMonitor  
IPOPTOptions  
RuntimeOptions  
アプリケーション  
関連項目
テクニカルノート
関連するガイド
引用書式
IPOPTLink`
IPOPTLink`

IPOPTMinimize

IPOPTMinimize[f,{x1,…},{x1i0,…}]

xj についての f の極小値をxj=xj0 から始めて数値的に検索する．

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…}]

変数境界制約条件 xj min≤xj≤xj max の下で極小値を数値的に検索する．

IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…}]

関数制約条件 gi min≤gi(x)≤gi max の下で極小値を数値的に検索する

詳細とオプション

  • IPOPTMinimizeを使うにはまずNeeds["IPOPTLink`"]を使ってそれをロードする必要がある．
  • IPOPTMinimizeは，変数の境界制約条件および／または関数の制約条件の下で，目的関数 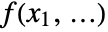の実数値の極小化問題を数値的に解く．
  • 目的関数 f と制約条件関数{g1,…}は実数値で，2回連続微分可能でなければならない．
  • 最適化問題は凸状でも線形でもない必要がある．
  • 等式制約条件 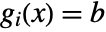は制約条件の境界を{b,b}と設定することで指定できる． »
  • IPOPTMinimizeは解のオブジェクトをIPOPTData式の形で返す．
  • IPOPTMinimizeには以下のオプションが与えられる：
  • StepMonitor Noneステップを取るときに評価する式
    IPOPTOptions {}IPOPTライブラリに渡されるオプション
    RuntimeOptions Automaticランタイム設定を指定するオプション
  • IPOPTライブラリオプションには文字列名と，実数，整数，文字列の値がある．
  • IPOPTOptionsに指定できるオプションの例：
  • "tol"real希望する収束許容範囲（相対的）
    "max_iter"integer許可される最大繰返し回数
    "linear_solver"string使用する線形ソルバ（例："mumps"）
  • IPOPTライブラリオプションすべてとその可能な値のリストはWebページに掲載されている．

例題

すべて開く すべて閉じる

例  (3)

から始めて，の極小値を求める．

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {1, 1}]

IPOPTData式から極小値とその位置を抽出する：

Wolfram Language code: {fmin, minpt} = {IPOPTMinValue[sol], IPOPTArgMin[sol]}

解をプロットする：

Wolfram Language code: Show[Plot3D[Cos[x + y] * Sin[x - y], {x, 0, 3}, {y, 0, 3}, PlotStyle -> Opacity[0.5]], Graphics3D[{Red, PointSize[.04], Point[Join[minpt, {fmin}]]}]]

変数の境界が，である場合に，から始めて，を極小化する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {1, 1}, {{0, 2}, {0, 2}}]

IPOPTData式から極小値とその位置を抽出する：

Wolfram Language code: {fmin, minpt} = {IPOPTMinValue[sol], IPOPTArgMin[sol]}

解をプロットする：

Wolfram Language code: Show[Plot3D[Cos[x + y] * Sin[x - y], {x, 0, 2}, {y, 0, 2}, PlotStyle -> Opacity[0.5]], Graphics3D[{Red, PointSize[.04], Point[Join[minpt, {fmin}]]}]]

変数の境界が，，関数の制約条件がである場合に，から始めて，を極小化する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {1, 1}, {{0, 3}, {0, 3}}, {x ^ 2 + y ^ 2}, {{0, 4}}]

IPOPTData式から極小値とその位置を抽出する：

Wolfram Language code: {fmin, minpt} = {IPOPTMinValue[sol], IPOPTArgMin[sol]}

解をプロットする：

Wolfram Language code: f[{x_, y_}] := Cos[x + y] * Sin[x - y]; cpts = N[2CirclePoints[500]];Show[Plot3D[Cos[x + y] * Sin[x - y], {x, 0, 3}, {y, 0, 3}, PlotStyle -> Opacity[0.5]], ListPointPlot3D[Join[#, {f[#]}]& /@ cpts, PlotStyle -> PointSize[.015]], Graphics3D[{Red, PointSize[.04], Point[Join[minpt, {fmin}]]}]]

スコープ  (2)

目的関数の負数を極小化することによって，関数を極大化する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[-Sin[x + y], {x, y}, {0, 0}, {{0, 1}, {0, 1}}]

IPOPTData式から極大値とその位置を求める：

Wolfram Language code: {-IPOPTMinValue[sol], IPOPTArgMin[sol]}

等しい上下界を指定することで，関数を等式制約条件 で極小化する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {1, 0}, {{0, 1}, {0, 1}}, {x ^ 2 + y ^ 2}, {{1, 1}}]

IPOPTData式から極小値とその位置を抽出する：

Wolfram Language code: {fmin, minpt} = {IPOPTMinValue[sol], IPOPTArgMin[sol]}

オプション  (5)

StepMonitor  (1)

関数の極小値を求める際にIPOPTMinimizeが取ったステップ：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {0, 1}, {{-1, 1}, {-1, 1}}, StepMonitor :> Print[{x, y}]]

IPOPTOptions  (2)

IPOPTライブラリのドキュメント(http://www.coin-or.org/Ipopt/documentation/node39.html)に記載されているように，IPOPTOptionsを使ってオプションを設定する：

"tol"を使って相対許容誤差を10.^-6に設定する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {0, 1}, {{-1, 1}, {-1, 1}}, "IPOPTOptions" -> {"tol" -> 10. ^ -6}]

このオプションを指定すると，およそ6桁精度が期待できる：

Wolfram Language code: {IPOPTMinValue[sol], IPOPTArgMin[sol]}

厳密解と比較する：

Wolfram Language code: N[{-1, {-Pi / 4, Pi / 4}}]

"max_iter"を使って最大繰返し回数を5に設定する：

Wolfram Language code: Needs["IPOPTLink`"]
Wolfram Language code: sol = IPOPTMinimize[Cos[x + y] * Sin[x - y], {x, y}, {0, 1}, {{-1, 1}, {-1, 1}}, "IPOPTOptions" -> {"max_iter" -> 5}]

上記誤差は，デフォルトの許容誤差10^-8を満足するためには，繰返し回数が十分でなかったことを示唆する：

Wolfram Language code: {Abs[IPOPTMinValue[sol] - (-1)] / 1, Abs[IPOPTArgMin[sol] - {-Pi / 4, Pi / 4}] / (Pi / 4)}

RuntimeOptions  (2)

RuntimeOptionsはランタイム設定の指定に使用できる：

深刻なエラーが生じた際にIPOPTDataオブジェクトを返すか$Failedを返すかを"RuntimeErrorHandler"を使って指定する：

Wolfram Language code: Needs["IPOPTLink`"]

Automatic設定では，マシンのオーバーフロー等，エラーによっては$Failedが返される：

Wolfram Language code: sol = IPOPTMinimize[-Log[a * E ^ (1 - a)], {a}, {1000.}, {{0., 1.*^40}}]

IPOPTReturnCodeが抽出できるように解のオブジェクトを返す：

Wolfram Language code: sol = IPOPTMinimize[-Log[a * E ^ (1 - a)], {a}, {1000.}, {{0., 1.*^40}}, "RuntimeOptions" -> {"RuntimeErrorHandler" -> "ReturnObject"}]

戻りコードを抽出する：

Wolfram Language code: IPOPTReturnCode[sol]

ランタイムの問題を示す警告メッセージは"WarningMessges"で表示をオンにしたりオフにしたりできる：

Wolfram Language code: Needs["IPOPTLink`"]

警告メッセージの表示をオフにする：T

Wolfram Language code: sol = IPOPTMinimize[-Log[a * E ^ (1 - a)], {a}, {1000.}, {{0., 1.*^40}}, "RuntimeOptions" -> {"WarningMessages" -> False}]

アプリケーション  (1)

直径が である 辺の多角形の面積が最大となるような多角形を求める．{r[i],t[i]}を多角形の頂点の極座標とする．変数とその境界は以下のようになる：

Wolfram Language code: n = 6; varranges = Join[Table[{t[i], 0., Infinity}, {i, n - 1}], Table[{r[i], 0, 1}, {i, n - 1}], {{t[n], π, π}, {r[n], 0., 0.}}]
Wolfram Language code: vars = Map[First, varranges]
Wolfram Language code: varbounds = Map[{#[[2]], #[[3]]}&, varranges]

多角形の面積は以下のようになる：

Wolfram Language code: area = .5 Sum[r[i] r[i - 1] Sin[t[i] - t[i - 1]], {i, 2, n}]

極小化問題を使って記述するために，目的関数の負数を取る：

Wolfram Language code: objfn = -area;

制約条件と制約境界を設定する：

Wolfram Language code: constr1 = Flatten[Table[0. ≤ r[i] ^ 2 + r[j] ^ 2 - 2 r[i] r[j] Cos[t[i] - t[j]] ≤ 1, {i, 1, n}, {j, i + 1, n}], 2]; constr2 = Table[-2. Pi ≤ t[i - 1] - t[i] ≤ 0, {i, 2, n}]; constr = Join[constr1, constr2]; constrbounds = Map[{#[[1]], #[[3]]}&, constr] constr = Map[#[[2]]&, constr]

極小化の開始点を定義する：

Wolfram Language code: x0 = vars /. {r[i_] -> 4. i (n + 1 - i) / (n + 1) ^ 2} /. {t[i_] -> π i / n}

パッケージをロードし，極小化問題を解く：

Wolfram Language code: Needs["IPOPTLink`"] sol = IPOPTMinimize[objfn, vars, x0, varbounds, constr, constrbounds]

解のオブジェクトから最大面積を抽出する：

Wolfram Language code: -IPOPTMinValue[sol]

解のオブジェクトから最適変数値を抽出する：

Wolfram Language code: ipoptsol = MapThread[Rule, {vars, IPOPTArgMin[sol]}]

直交座標における点を求める：

Wolfram Language code: ipoptrectpts = Table[{r[i] Cos[t[i]], r[i] Sin[t[i]]}, {i, 1, n}] /. ipoptsol

結果をプロットする

Wolfram Language code: Show[ListPlot[ipoptrectpts, PlotStyle -> {Blue, PointSize -> Large}], Graphics[{Opacity[.1], Blue, Polygon[ipoptrectpts]}], AspectRatio -> 1]
Wolfram Research (2016), IPOPTMinimize, Wolfram言語関数， https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

テキスト

Wolfram Research (2016), IPOPTMinimize, Wolfram言語関数， https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

CMS

Wolfram Language. 2016. "IPOPTMinimize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.

APA

Wolfram Language. (2016). IPOPTMinimize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html

BibTeX

@misc{reference.wolfram_2026_ipoptminimize, author="Wolfram Research", title="{IPOPTMinimize}", year="2016", howpublished="\url{https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html}", note=[Accessed: 19-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_ipoptminimize, organization={Wolfram Research}, title={IPOPTMinimize}, year={2016}, url={https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html}, note=[Accessed: 19-June-2026]}