IPOPTMinimize
IPOPTMinimize[f,{x1,…},{x1i0,…}]
numerically searches for a local minimum of f in xj, starting from the point xj=xj0.
IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…}]
numerically searches for a local minimum subject to the variable bound constraints xj min≤xj≤xj max.
IPOPTMinimize[f,{x1,…},{x1i0,…},{{x1min,x1max},…},{g1,…},{{g1min,g1max},…}]
numerically searches for a local minimum subject to function constraints gi min≤gi(x)≤gi max.
更多信息和选项
- To use IPOPTMinimize, you first need to load it using Needs["IPOPTLink`"].
- IPOPTMinimize numerically solves a real-valued minimization problem for an objective function
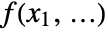subject to variable bound constraints and/or function constraints. - The objective f and the constraint functions {g1,…} should be real-valued and twice continuously differentiable.
- The optimization problem need not be convex or linear.
- Equality constraints
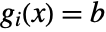may be specified by setting the constraint bounds to {b,b}. » - IPOPTMinimize returns a solution object in the form of an IPOPTData expression.
- The following options can be given to IPOPTMinimize:
-
StepMonitor None expression to evaluate whenever a step is taken IPOPTOptions {} options to be passed to the IPOPT library RuntimeOptions Automatic options to specify runtime settings - The IPOPT library options have string names and real, integer or string values.
- Example options that can be specified in IPOPTOptions include:
-
"tol" real desired convergence tolerance (relative) "max_iter" integer maximum number of iterations allowed "linear_solver" string linear solver to be used (e.g. "mumps") - The complete list of IPOPT library options and possible values can be found on the web page.
范例
打开所有单元关闭所有单元基本范例 (3)
Find a local minimum of 
starting from 
.
Extract the minimum value and position from the IPOPTData expression:
Minimize 
with variable bounds 
, 
, starting from 
.
Extract the minimum value and position from the IPOPTData expression:
Minimize 
with variable bounds 
, 
and function constraint 
, starting from 
.
Extract the minimum value and position from the IPOPTData expression:
Scope (2)
Maximize a function 
by minimizing the negative of the objective value:
Find the maximum value and position from the IPOPTData expression:
Minimize a function with an equality constraint 
by specifying equal lower and upper bounds 
:
Extract the minimum value and position from the IPOPTData expression:
Options (5)
IPOPTOptions (2)
Use IPOPTOptions to set options as described in the IPOPT library documentation http://www.coin-or.org/Ipopt/documentation/node39.html:
Use "tol" to set the relative error tolerance to 10.^-6:
With this option we can expect about 6 digits of precision:
Compare to the exact solution:
Use "max_iter" to set the maximum number of iterations to 5:
The error above indicates that the iterations were not enough to satisfy the default relative error tolerance of 10^-8:
RuntimeOptions (2)
Use RuntimeOptions to specify runtime settings:
Use "RuntimeErrorHandler" to indicate whether to return an IPOPTData object or $Failed when a serious error occurs:
With some errors such as machine overflow, $Failed is returned with the Automatic setting:
Return a solution object so that the IPOPTReturnCode can be extracted:
Use "WarningMessges" to turn off and on the warning messages indicating runtime problems:
Applications (1)
Find the polygon with maximal area among polygons with 
sides and diameter 
. Let {r[i],t[i]} be the polar coordinates of the vertices of the polygon. The variables and their bounds are:
To state as a minimization problem negate the objective function:
Set up the constraints and the constraint bounds:
Define an initial point for the minimization:
Load the package and solve the minimization problem:
Extract the maximum area from the solution object:
Extract the optimal variable values from the solution object:
文本
Wolfram Research (2016)，IPOPTMinimize，Wolfram 语言函数，https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.
CMS
Wolfram 语言. 2016. "IPOPTMinimize." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html.
APA
Wolfram 语言. (2016). IPOPTMinimize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/IPOPTLink/ref/IPOPTMinimize.html 年