QuadraticFormDistribution
QuadraticFormDistribution[{a,b,c},{μ,Σ}]
represents the distribution of a quadratic form z.a.z+b.z+c for multivariate normal z.
更多信息和选项
- To use QuadraticFormDistribution, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
- QuadraticFormDistribution is the distribution of z.a.z+b.z+c for real-valued
×
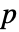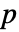symmetric positive definite matrix a, length-
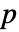vector b, scalar c, and 
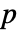-dimensional multivariate normal vector z. - QuadraticFormDistribution can be used with such functions as Mean and RandomReal.
范例
打开所有单元关闭所有单元Possible Issues (2)
PDF and CDF can only be evaluated using Series:
Series expansion must be about the lower support point for the distribution:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
文本
Wolfram Research (2007)，QuadraticFormDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/MultivariateStatistics/ref/QuadraticFormDistribution.html.
CMS
Wolfram 语言. 2007. "QuadraticFormDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/QuadraticFormDistribution.html.
APA
Wolfram 语言. (2007). QuadraticFormDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/MultivariateStatistics/ref/QuadraticFormDistribution.html 年