RegisterOptimizationMethod[method,assoc]
registers a convex solver with name method and Association assoc containing details of the solver capabilities.


RegisterOptimizationMethod
RegisterOptimizationMethod[method,assoc]
registers a convex solver with name method and Association assoc containing details of the solver capabilities.
Details and Options
- The solver name method should be a string. Once a solver is registered, it can be used in the Wolfram Language optimization functions by specifying Method->method.
- The following keys are considered in the Association assoc:
-
"SolveFunction" the function to evaluate to use the solver "Submethods" a list of registered submethods "ConstraintSupport" a list of the support for constraints "ObjectiveSupport" the type of objective function supported by the method "MixedIntegerSupport" whether or not the solver works with mixed integer problems "ExtendedPrecisionSupport" whether the method supports extended precision "FreeMethodDataFunction" a function to evaluate when the solver data is no longer needed "MessageHandling" how to handle any messages generated by the solver - The value associated with "ObjectiveSupport" should be one of the following:
-
"Linear" linear objective 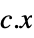
"Quadratic" quadratic objective 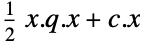
"Nonlinear" general nonlinear objective - If "ObjectiveSupport" is not specified, the support is assumed to be linear.
- The value associated with "ConstraintSupport" should be an association where the keys are the constraint forms supported and the values are the type of support of that list of rules ctype->stype, where ctype describes the constraint type and stype describes the support type.
- The constraint type ctype can be any of the following:
-
"LinearEqualityConstraint" linear equality constraints "NonNegativeCone" linear inequality constraints "NormCone" second order cone constraints "SemidefiniteCone" positive semidefinite constraints "ExponentialCone" exponential cone constraints "DualExponentialCone" dual exponential cone constraints "PowerCone" power cone constraints "DualPowerCone" dual power cone constraints "QuadraticConstraint" quadratic constraints "NonlinearConstraint" general nonlinear constraints - The support type stype can be one of the following:
-
"Affine" 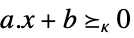
"Membership" 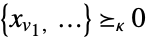
"LinearMatrixInequality" ![a_(1) x_(1)+...+a_(k) x_(k)+b>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_(1) x_(1)+...+a_(k) x_(k)+b>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/RegisterOptimizationMethod.en/5.png) (SemidefiniteCone only)
(SemidefiniteCone only)"SplitAffine" separate semidefinite constraints by block structure of the linear matrix inequality (Semidefinite cone only) - The value associated with "MessageHandling" should be one of the following:
-
"Collect" collect messages (this is the default) "Issue" issue messages immediately from when they are generated "Suppress" suppress any messages generated by the solver - With the default value "Collect", messages are collected by the code and issued when the solution is complete. The message tag is modified to the function that is calling the solver.
- The value associated with "ExtendedPrecisionSupport" should be one of the following:
-
False machine precision only (this is the default) True the method can work with extended precision numbers All the method can work with exact numerical computations - If the value associated with "ExtendedPrecisionSupport" is True or All the solve function should accept a WorkingPrecision option.
- The value sfun associated with the "SolveFunction" key is the main interface to the Wolfram Language convex optimization functions. When an optimization function is used with Method->method, then sfun[problemData,opts] is evaluated.
- Evaluation of sfun[problemData,opts] should return a list, {status,methodData}.
- The problemData Association is constructed by the Wolfram Language convex optimization functions to correspond to the problem:
-
minimize 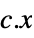
subject to constraints 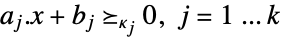
- The problem is described using the following keys:
-
"ObjectiveVector" 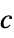
"ObjectiveMatrix" quadratic matrix 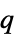 if "ObjectiveSupport" is "Quadratic"
if "ObjectiveSupport" is "Quadratic""ObjectiveFunction" nonlinear objective function 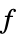
"ConstraintSpecifications" 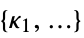
"ConstraintCoefficientArrays" 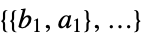
"IntegerVariableColumns" a list of the column indexes for any components of 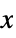 that are expected to be integers.
that are expected to be integers."ConeVariableColumns" a list of the variable columns associated with each conic contraint that requires variable membership "ExtraColumns" the number of extra columns added to convert to conic constraints with variable membership "Caller" the Wolfram Language function the solver is being called from - The status should be one of:
-
Success["Solved",assoc] the problem was solved Success["Unbounded",assoc] the problem was unbounded Success["Infeasible",assoc] the problem was infeasible Failure[reason,assoc] the solver failed to solve the problem because of reason - When the status has a Head of Success, there should be definitions for the following solution properties:
-
methodData["PrimalMinimizerVector"] 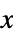
methodData["PrimalMinimumValue"] 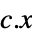
methodData["DualMaximizer"] 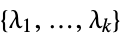
methodData["DualMaximumValue"] 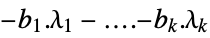
methodData["Slack"] 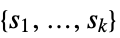 (will be computed automatically if not defined)
(will be computed automatically if not defined) - The options that will be given to the solver function in sfun[problemData, opts] may be any options that the solver uses as method options in addition to the options given to the Wolfram Language optimization function:
-
MaxIterations Automatic maximum number of iterations to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons WorkingPrecision MachinePrecision the precision to use - Further details and examples can be found in the tutorial Optimization Method Framework.
Examples
Basic Examples (1)
Register a toy method for quadratically constrained quadratic problems with any working precision.
Load the OptimizationMethodFramework` package:
Register a method named "QCQPExact" as an optimization solver method:
This registers a solver named "QCQPExact" with a solve function named QCQPExactSolve, for problems with quadratic objective ![]() and constraints that can be vector equality
and constraints that can be vector equality ![]() , vector inequality
, vector inequality ![]() , norm cone constraints
, norm cone constraints ![]() or quadratic constraints
or quadratic constraints ![]() where
where ![]()
![]()
![]() and
and ![]() are
are ![]() symmetric positive semidefinite matrices,
symmetric positive semidefinite matrices,![]() It supports machine precision, extended precision and infinite precision.
It supports machine precision, extended precision and infinite precision.
Define a function to convert affine vector equality, vector inequality, norm cone and quadratic constraints into regular equality and inequality constraints:
Define the main solver function. It constructs arguments for the function Minimize and records the solution in QCQPExactSolutionData:
Set up rules for the solution properties:
Tech Notes
Text
Wolfram Research (2020), RegisterOptimizationMethod, Wolfram Language function, https://reference.wolfram.com/language/OptimizationMethodFramework/ref/RegisterOptimizationMethod.html.
CMS
Wolfram Language. 2020. "RegisterOptimizationMethod." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/OptimizationMethodFramework/ref/RegisterOptimizationMethod.html.
APA
Wolfram Language. (2020). RegisterOptimizationMethod. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/OptimizationMethodFramework/ref/RegisterOptimizationMethod.html
BibTeX
@misc{reference.wolfram_2025_registeroptimizationmethod, author="Wolfram Research", title="{RegisterOptimizationMethod}", year="2020", howpublished="\url{https://reference.wolfram.com/language/OptimizationMethodFramework/ref/RegisterOptimizationMethod.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_registeroptimizationmethod, organization={Wolfram Research}, title={RegisterOptimizationMethod}, year={2020}, url={https://reference.wolfram.com/language/OptimizationMethodFramework/ref/RegisterOptimizationMethod.html}, note=[Accessed: 18-February-2026]}