is a symbol used to indicate machine‐number precision.


MachinePrecision
is a symbol used to indicate machine‐number precision.
Details
- The numerical value of MachinePrecision is $MachinePrecision.
- Precision[1.] gives MachinePrecision.
- MachinePrecision is the default specification for precision in N and other numerical functions.
- Approximate real numbers are assumed to have precision specified by MachinePrecision if fewer than $MachinePrecision explicit digits are entered.
- The option setting WorkingPrecision->MachinePrecision specifies that internal computations in numerical functions should be done with machine numbers.
- MachinePrecision is treated as a numeric constant, with attribute Constant.
Background & Context
- MachinePrecision is the symbol representing the number of decimal digits used by numerical functions such as N, NIntegrate, and NSum in the Wolfram Language for machine-precision computations. The numerical value of MachinePrecision is given by $MachinePrecision, which is itself a machine-precision number equal to
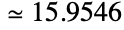 . When used as a symbolic expression, MachinePrecision is treated as an exact numeric quantity with value 53/Log2[10], corresponding to 53 binary digits of precision.
. When used as a symbolic expression, MachinePrecision is treated as an exact numeric quantity with value 53/Log2[10], corresponding to 53 binary digits of precision. - In general, numerical and graphical functions in the Wolfram Language take one or more precision options that control the desired numerical precision to be used in a computation. The most common such options are WorkingPrecision (which specifies the number of digits of precision that should be maintained in internal computations) and PrecisionGoal (which specifies how many effective digits of precision should be sought in the final result). MachinePrecision is the default working precision value for all plotting functions, for most numerical functions, and also for Compile (both when invoked explicitly and when called behind-the-scenes during autocompilation).
- Machine-precision numbers (often called simply "machine numbers") always contain a fixed number of digits and maintain no information about precision. While the exponent and significand can be stored independently for such numbers, their "scale" remains constrained by the possible range of exponents. Arithmetic using this sort of fixed-precision numbers is known as floating-point computation and is most commonly implemented using the IEEE Standard for Floating-Point Arithmetic (IEEE 754) standard. Machine-precision computations are typically performed using native floating-point unit and low-level numeric library operations that are typically very fast (particularly so in matrix arithmetic), but provide no tracking of precision loss that may occur due to numerical round-off and other factors during a computation. As a result, machine arithmetic gives fast but numerically unvalidated results that may differ substantially from correct values.
- In addition to machine arithmetic, the Wolfram Language allows numerical computation by means of "significance arithmetic" involving precision-tagged "arbitrary-precision" numbers. As their name implies, arbitrary-precision numbers may contain an arbitrary number of digits and, as a result, can include precision information that can be propagated through a computation. Using this technique, a final numerical result may be returned that has fewer digits of precision than the original input, but for which the digits that are returned are numerically validated.
- MachinePrecision is the default precision goal (i.e. desired precision in the final result) for the special numericization function N. Using N[expr] is therefore equivalent to setting prec to MachinePrecision in the two-argument form N[expr,prec]. It is important to understand that specifying prec as the symbol MachinePrecision is completely different from specifying its numerical value $MachinePrecision. In particular, the former will numericize to a machine number, while the latter will numericize to an arbitrary-precision number with the specified number of significant digits. For example, N[Pi,MachinePrecision] and N[Pi,$MachinePrecision] give different outputs. InputForm or FullForm can be used to see the underlying numerical representations, which consist of a decimal number with 16 or fewer digits for a machine number and an expression of the form digits`prec for an arbitrary-precision number. The underlying binary digits for either a machine-precision or arbitrary-precision number can be extracted using RealDigits[expr,2].
- To specify an explicit numeric precision prec for a number, the number may be entered using the "back-tick" syntax digits`prec. More generally, SetPrecision[expr,prec] can be used to return a version of expr in which all numbers have been set to have precision prec, and where prec may be specified as a number, MachinePrecision, or Infinity. A special case is given by the approximate number 0., which does not carry a precision and hence is coerced back to a machine number even when given any explicit finite precision. Precision[expr] can be used to find the numeric precision of a given expression.
- Numbers specified using a small number of explicit digits are assumed to have machine precision, meaning for example that Precision[0.123] returns MachinePrecision. More generally, approximate real numbers are assumed to have precision specified by MachinePrecision if fewer than $MachinePrecision explicit digits are entered on input. If more digits are specified, the number is assigned a precision corresponding to the number of digits specified (cf. Precision[0.12345678901234567] versus Precision[0.123456789012345678]).
- In calculations that contain both arbitrary- and machine-precision numbers, all numbers are coerced to machine precision as needed. Furthermore, this coercion is carried out even if the arbitrary-precision numbers have precision smaller than MachinePrecision (e.g. N[E,30] + N[Pi] and N[E,3] + N[Pi] both return machine numbers). Furthermore, in calculations that request MachinePrecision but for which the resulting numbers are too big or too small to be represented using 53 bits, results are automatically returned as arbitrary-precision numbers (e.g. N[Exp[1000],MachinePrecision]).
- Both machine- and arbitrary-precision numbers of the same type have the same Head (e.g. Real or Complex). However, machine-precision numbers display a fixed maximum number of digits in StandardForm (the default value is 6, but it can be changed in the Preferences menu), whereas arbitrary-precision numbers display all significant digits. MachineNumberQ[expr] returns True if expr is a machine‐precision real or complex number and False otherwise. Other useful functions for testing numbers and expressions include NumberQ, NumericQ, ExactNumberQ, and InexactNumberQ.
Examples
open all close allBasic Examples (2)
MachinePrecision is treated as an exact numeric quantity:
Scope (2)
Applications (3)
Properties & Relations (4)
Numbers with just a few digits entered are assumed to have machine precision:
Precision is based on the number of digits when more than $MachinePrecision+1 are entered:
MachinePrecision is a numerical constant while $MachinePrecision evaluates to a number:
MachinePrecision is numerically Equal to $MachinePrecision:
$MachinePrecision is the machine-precision approximation to MachinePrecision:
MachinePrecision times the number of bits per digit gives the binary machine precision:
Digits beyond the known precision are represented as Indeterminate:
Possible Issues (2)
Subnormal machine numbers have precision MachinePrecision:
However, they effectively have less precision and have the same uncertainty as $MinMachineNumber:
Subnormal machine numbers entered in InputForm will drop non-representable digits:
Enter as an arbitrary-precision number to keep all the digits:
See Also
Tech Notes
Related Guides
History
Introduced in 2003 (5.0)
Text
Wolfram Research (2003), MachinePrecision, Wolfram Language function, https://reference.wolfram.com/language/ref/MachinePrecision.html.
CMS
Wolfram Language. 2003. "MachinePrecision." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MachinePrecision.html.
APA
Wolfram Language. (2003). MachinePrecision. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MachinePrecision.html
BibTeX
@misc{reference.wolfram_2025_machineprecision, author="Wolfram Research", title="{MachinePrecision}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/MachinePrecision.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_machineprecision, organization={Wolfram Research}, title={MachinePrecision}, year={2003}, url={https://reference.wolfram.com/language/ref/MachinePrecision.html}, note=[Accessed: 12-March-2026]}