Optimization`MethodFramework`

RegisterOptimizationMethod

RegisterOptimizationMethod[method,assoc]

名前 method および，ソルバ機能の詳細を含む Association assoc で凸ソルバを登録する．

詳細とオプション

ソルバ名 method は文字列でなければならない．ソルバが登録されると，Method->method と指定することでWolfram言語の最適化関数で使えるようになる．
Association assoc で考えられるキーは以下の通りである：

	"SolveFunction"	ソルバを使うために評価する関数
	"Submethods"	登録されたサブメソッドのリスト
	"ConstraintSupport"	制約に対するサポートのリスト
	"ObjectiveSupport"	メソッドによってサポートされる目的関数のタイプ
	"MixedIntegerSupport"	ソルバが混合整数計画問題に使えるかどうか
	"ExtendedPrecisionSupport"	メソッドが拡張精度をサポートするかどうか
	"FreeMethodDataFunction"	ソルバのデータがそれ以上必要ではなくなったときに評価する関数
	"MessageHandling"	ソルバによって生成されたメッセージを扱う方法

"ObjectiveSupport"に関連付けられる値は以下のいずれか一つである：
"Linear" 線形目的関数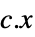

"Quadratic" 二次目的関数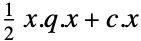

"Nonlinear" 一般的な非線形目的関数
"ObjectiveSupport"が指定されたいない場合は，サポートは線形とみなされる．
"ConstraintSupport"に関連付けられる値は連想である．キーはサポートされる制約の形式，値は規則 ctype->stype のそのリストのサポートタイプである．ここで ctype は制約のタイプ，stype はサポートタイプである．
制約タイプ ctype は以下のいずれかで与えることができる：

	"LinearEqualityConstraint"	線形等式制約
	"NonNegativeCone"	線形不等式制約
	"NormCone"	二次錐制約
	"SemidefiniteCone"	半正定値制約
	"ExponentialCone"	指数錐制約
	"DualExponentialCone"	双対指数錐制約
	"PowerCone"	power cone制約
	"DualPowerCone"	双対power cone制約
	"QuadraticConstraint"	二次制約
	"NonlinearConstraint"	一般的な非線形制約

サポートタイプ stype は以下のいずれか一つである：

	"Affine"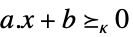
	"Membership"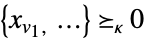
	"LinearMatrixInequality"	$a_(1) x_(1)+...+a_(k) x_(k)+b>=_(TemplateBox[{n}, SemidefiniteConeList])0$ （半正定値錐のみ）
	"SplitAffine"	線形行列不等式のブロック構造による，別の半正定値制約（半正定値錐のみ）

"MessageHandling"に関連付けられる値は以下のいずれか一つである：

	"Collect"	メッセージを収集する（デフォルト）
	"Issue"	メッセージが生成されたときに直ちにメッセージを発する
	"Suppress"	ソルバによって生成されたすべてのメッセージを非表示にする

デフォルト値の"Collect"では，メッセージはコードによって収集され，解き終ったときに表示される．ソルバを呼び出す関数のメッセージタグは変更することができる．
"ExtendedPrecisionSupport"に関連付けられる値は以下のいずれか一つである：
False 機械精度のみ（デフォルト）

True メソッドは拡張精度数が使える

All メソッドは厳密な数値計算が使える
"ExtendedPrecisionSupport"に関連付けられた値がTrueかAllならば，solve関数はWorkingPrecisionオプションを受け入れる．
"SolveFunction"キーに関連付けられた値 sfun は，Wolfram言語の凸最適化関数のメインのインターフェースである．最適化関数がMethod->method で使われる場合，sfun[problemData,opts]が評価される．
sfun[problemData,opts] を評価するとリスト{status,methodData}が戻る．
problemData Associationは以下の問題に対応するために，Wolfram言語の凸最適化関数によって構築される：
最小化する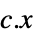

次の制約に従う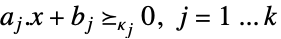
問題は以下のキーを使って記述される：

	"ObjectiveVector"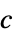
	"ObjectiveMatrix"	"ObjectiveSupport"が"Quadratic"ならば，二次行列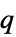
	"ObjectiveFunction"	非線形目的関数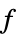
	"ConstraintSpecifications"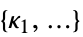
	"ConstraintCoefficientArrays"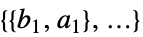
	"IntegerVariableColumns"	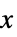のすべての成分についての列番号のリストであり，整数と想定される
	"ConeVariableColumns"	変数のメンバーシップを要求する各錐制約に関連付けられた変数列のリスト
	"ExtraColumns"	変数メンバーシップを持つ錐制約に変換するために加えられた追加列の数
	"Caller"	ソルバを呼び出すWolfram言語関数

状態は以下のいずれかである：

	Success["Solved",assoc]	問題が解かれた
	Success["Unbounded",assoc]	問題が非有界であった
	Success["Infeasible",assoc]	問題が実行不可能であった
	Failure[reason,assoc]	ある理由(reason)のためにソルバは問題が解けなかった

状態のHeadがSuccessの場合，以下の解の特性の定義がある：

	methodData["PrimalMinimizerVector"]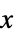
	methodData["PrimalMinimumValue"]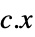
	methodData["DualMaximizer"]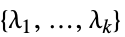
	methodData["DualMaximumValue"]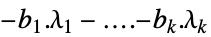
	methodData["Slack"]	（定義されていない場合は自動的に計算される）

sfun[problemData, opts]のソルバ関数に与えられるオプションは，Wolfram言語の最適化関数に与えられるオプションに加え，ソルバがメソッドオプションとして使う任意のオプションである：

MaxIterations	Automatic	使用する最大反復回数
PerformanceGoal	$PerformanceGoal	最適化を試みるパフォーマンスの局面
Tolerance	Automatic	内部比較に使う許容度
WorkingPrecision	MachinePrecision	使用する精度

詳細と例題は，チュートリアル「最適化メソッドフレームワーク」をご覧いただきたい．

例題

例 (1)

二次制約付きの二次問題のためのメソッドを任意の作業精度で登録する．

OptimizationMethodFramework`パッケージを登録する：

"QCQPExact"というメソッドを最適化ソルバメソッドとして登録する：

これで，二次目的関数および制約を持つ問題に対する"QCQPExact"というソルバが，QCQPExactSolveというsolve関数で登録される．この制約はベクトルの等式，ベクトルの不等式，ノルム錐制約，二次制約いずれでもあり得る．ここではの対称正定値行列である．このソルバは機械精度，拡張精度，無限精度をサポートする．