Acoustic Mirror
| Introduction | Initial and Boundary Conditions |
| Pressure Acoustics Model | Solve the PDE Model |
| Domain | Post-processing and Visualization |
| Sound Source | Nomenclature |
| Mesh Generation | References |
Introduction
An acoustic mirror is a passive device that collects and amplifies sound waves. They are often designed in a parabolic shape made of sound hard materials, which allows them to reflect and focus incident sound signals. Before the invention of the radar system, acoustic mirrors were used to detect incoming aircraft. In recent years, due to its simple setup and efficiency in signal processing [1], acoustic mirrors have been commonly used in aeroacoustic wind tunnels for noise measurement.
This study simulates the sound propagation across the paired sound mirrors. To visualize the scattering and refocusing patterns of the inharmonic sound signal, the acoustic PDE model is constructed in the time domain. However, the usage of the Fourier transform can quantify the performance of the mirrors in both the time and frequency domains. The modeling process also demonstrates the techniques on mesh refinement and the setup of sound sources.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Please refer to the information provided in "Acoustics in the Time Domain" for more general theoretical background for acoustics.
Pressure Acoustics Model
In this example, the propagation of sound waves can be described by the wave equation (2):
Domain
In the geometric model, a pair of parabolic sound mirrors is installed at ![]() and
and ![]() . Each mirror is designed to have a width
. Each mirror is designed to have a width ![]() and a focal length
and a focal length ![]() . At the focus of the left parabolic mirror, there is a monopole sound source. At the focus of the right parabolic mirror, there is a receiver.
. At the focus of the left parabolic mirror, there is a monopole sound source. At the focus of the right parabolic mirror, there is a receiver.
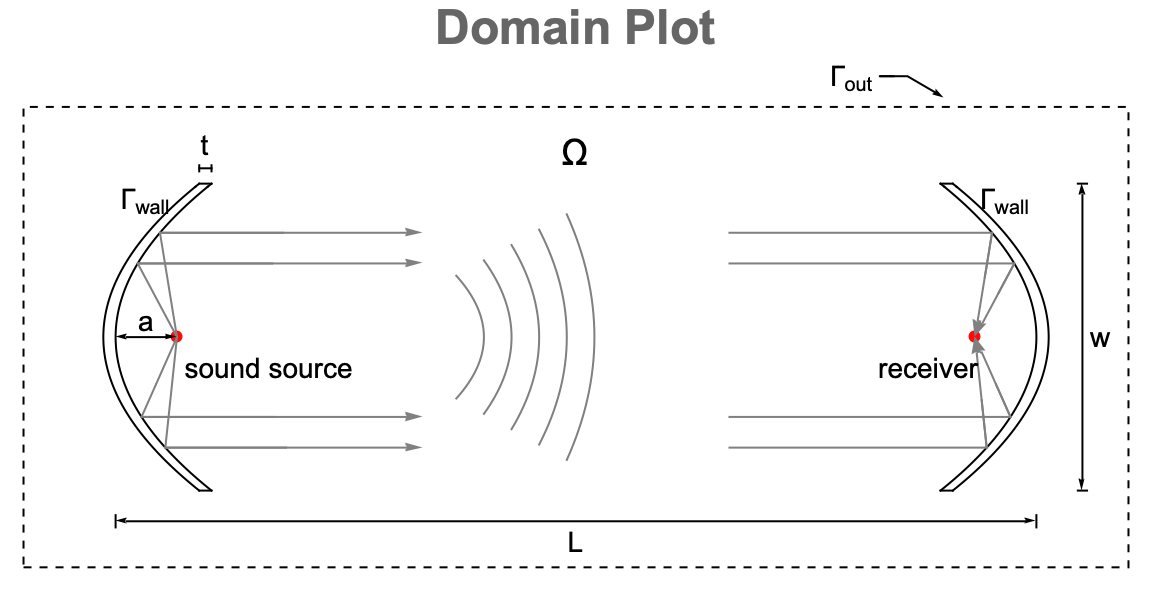
When the input signal originates from the left focus, the sound wave reflects off the left mirror and propagates to the direction the mirror is pointing, sending the sound signal across to the paired mirror. The incoming wave then reaches the right mirror, which reflects and refocuses the signal toward the receiver.
Subtracting the paired sound mirrors from a 2D rectangular domain ![]() specifies the simulation domain
specifies the simulation domain ![]() . In the domain plot, the solid lines denote wall boundaries
. In the domain plot, the solid lines denote wall boundaries ![]() modeling the surfaces of the mirrors, and the dashed lines model an outlet boundary
modeling the surfaces of the mirrors, and the dashed lines model an outlet boundary ![]() where the waves leave the domain.
where the waves leave the domain.
Sound Source
In this model, a point monopole source ![]() is placed on the left focus and a Gaussian derivative pulse is used as the time-inharmonic sound input. As will be shown in the next section, a Gaussian derivative pulse has a smooth and bounded frequency spectrum, which makes it a favorable source signal for the analytical purpose.
is placed on the left focus and a Gaussian derivative pulse is used as the time-inharmonic sound input. As will be shown in the next section, a Gaussian derivative pulse has a smooth and bounded frequency spectrum, which makes it a favorable source signal for the analytical purpose.
As explained in the acoustics time domain tutorial, a monopole source term ![]() is written as:
is written as:
… where ![]() is a regularized Dirac delta function at the source location
is a regularized Dirac delta function at the source location ![]() .
.
Mesh Generation
In acoustics simulations, the wavelength ![]() of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here the max edge length is set to 3 nodes per
of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here the max edge length is set to 3 nodes per ![]() , which means that there will be at least three elements per wavelength
, which means that there will be at least three elements per wavelength ![]() in each direction of the wave propagation:
in each direction of the wave propagation:
For the time-harmonic wave, the calculation of ![]() is straightforward. However, for the time-inharmonic wave that contains multiple frequencies, the wavelength
is straightforward. However, for the time-inharmonic wave that contains multiple frequencies, the wavelength ![]() in (3) is not explicitly specified. The rule to determine the mesh size
in (3) is not explicitly specified. The rule to determine the mesh size ![]() is to ensure that each frequency component is well resolved, which poses the following constraint:
is to ensure that each frequency component is well resolved, which poses the following constraint:
A common way to find the maximal frequency ![]() is to convert the input signal into the frequency domain with the Fourier transform.
is to convert the input signal into the frequency domain with the Fourier transform.
It is seen that the input signal is mostly constrained in the frequency range ![]() . The maximal frequency to resolve is then chosen to be
. The maximal frequency to resolve is then chosen to be ![]() .
.
Initial and Boundary Conditions
Since the sound signal begins with an undisturbed domain, the initial sound pressure ![]() and its derivative are set to zero.
and its derivative are set to zero.
There are two types of boundary conditions involved in this example. On the outer boundary ![]() , an absorbing boundary condition is specified to model the outgoing sound wave.
, an absorbing boundary condition is specified to model the outgoing sound wave.
On the wall boundary ![]() of the sound mirror, a default sound hard boundary conditions is implicitly used.
of the sound mirror, a default sound hard boundary conditions is implicitly used.
Solve the PDE Model
To study the full process of the wave scattering and refocusing by the sound mirror, the simulation time is set to ![]() . The PDE model is solved numerically with NDSolveValue using the finite element method.
. The PDE model is solved numerically with NDSolveValue using the finite element method.
Evaluating this simulation will require a larger-than-typical amount of RAM memory. Evaluating the simulation on a computer with insufficient memory will not work.
Post-processing and Visualization
Sound Pressure Distribution
To analyze the effect of the sound mirror, the sound propagation is first visualized in the time domain.
See this note about improving the visual quality of the animation.
At first, the monopole source on the left focus radiates sound waves in all directions. The left part of the wave hits the mirror and is then reflected to form the right-going plane wave. As the wave reaches the right mirror, it is reflected once more and concentrated toward the receiver.
To quantify the performance of the acoustic mirror, the sound pressure level at the receiver can be compared to the case without the mirror—that is, the free-space scattering wave.
First, the traveling time of the sound signal needs to be determined in both cases. For the free-space propagating wave, the time to reach the receiver is simply calculated by ![]() . In the case with acoustic mirrors, however, the traveling time of the refocusing signal is extended due to the reflection, which is given by
. In the case with acoustic mirrors, however, the traveling time of the refocusing signal is extended due to the reflection, which is given by ![]() .
.
With the traveling time computed, the pressure field of the free-space scattering wave [4] can be calculated analytically by:
Here ![]() denotes the input signal and
denotes the input signal and ![]() represents the distance between the sound source and the receiver.
represents the distance between the sound source and the receiver.
The sound signal is better preserved by the acoustic mirror (blue line) in comparison to the case without a mirror (orange line). The effectiveness of the mirror can be further enhanced by increasing the width of the mirror.
Quantifying the mirror performance is done by computing the amplification ratio ![]() , where
, where ![]() stands for the maximum sound pressure of the signal.
stands for the maximum sound pressure of the signal.
Compared to the free-space scattering wave, the sound signal with the acoustic mirror has been enhanced about three times at the receiver.
Sound Pressure Spectrum
Although the acoustic PDE model is constructed in the time domain to simulate the inharmonic sound input, it is still possible to study the effect of the acoustic mirrors in the frequency domain. To do so, a discrete Fourier transform (DFT) is used to convert the transient sound signal into the frequency spectrum. By visualizing the distribution of the frequency components, the performance of the acoustic mirror can be shown over the selected frequency range: ![]() .
.
To apply the DFT, the acoustic signal is sampled into a discrete list of sound pressure values.
As explained in a separate tutorial, the discrete Fourier transform generates ![]() Fourier coefficients
Fourier coefficients ![]() with a corresponding frequency component
with a corresponding frequency component ![]() . The frequency resolution of the Fourier transform is then given by
. The frequency resolution of the Fourier transform is then given by ![]() .
.
For the frequency range of ![]() , however, the data length
, however, the data length ![]() results in a coarse resolution
results in a coarse resolution ![]() that is not applicable for analysis. To improve the frequency resolution, the time domain dataset is extended with zeros for
that is not applicable for analysis. To improve the frequency resolution, the time domain dataset is extended with zeros for ![]() . This method [5] is also known as "zero padding".
. This method [5] is also known as "zero padding".
To achieve a frequency resolution of ![]() , the extended dataset should have a length of
, the extended dataset should have a length of ![]() points.
points.
With the acoustic mirror, the spectrum of the refocused sound wave has been squeezed toward the center around ![]() . That is, the acoustic mirror tends to preserve the central frequency components of the incoming signal but loses the ones with higher or lower frequencies. To increase the amplification on both ends of the spectrum [6], a wider mirror can be used, and the curvature of the mirror can also be adjusted based on sound source location.
. That is, the acoustic mirror tends to preserve the central frequency components of the incoming signal but loses the ones with higher or lower frequencies. To increase the amplification on both ends of the spectrum [6], a wider mirror can be used, and the curvature of the mirror can also be adjusted based on sound source location.
Nomenclature
| Symbol | Description | Unit |
| ρ | density | [kg/m3] |
| c | speed of sound | [m/s] |
| p | sound pressure | [Pa] |
| t | time | [s] |
| X | position vector | [m] |
| F | optional dipole source | [N/m3] |
| Q | optional monopole source | [1/s2] |
| w | mirror width | [m] |
| a | focal length | [m] |
| L | separation distance | [m] |
| Γwall | wall boundary | N/A |
| Γout | far-field boundary | N/A |
| Ω | computational domain | N/A |
| Ωrec | computational domain without mirrors | N/A |
| τ | half-pulse width | [s] |
| Xs | sound source location | [m] |
| h | mesh spacing | [m] |
| λ | sound wavelength | [m] |
| f | sound wave frequency | [Hz] |
| ω | sound wave angular frequency | [rad/s] |
| tfree | traveling time of free-space signal | [s] |
| tfree | traveling time of refocusing signal | [s] |
| ui | Fourier coefficient | N/A |
| fi | frequency component | [Hz] |
| d f | frequency resolution | [Hz] |
References
1. F. Ihlenburg. "The Medium-Frequency Range in Computational Acoustics: Practical and Numerical Aspects." Journal of Computational Acoustics, 11(2), 2003 pp. 175–193.
2. M. Helfer. "Sound Source Localisation with Acoustic Mirrors." From NAG/DAGA 2009 - Rotterdam, 2009 pp. 1432–1435.
3. F. Lindsten. "A Remark on Zero-Padding for Increased Frequency Resolution." 2010.
4. D. A. Russell, , J. P. Titlow and Y.-J.Bemmen. "Acoustic Monopoles, Dipoles and Quadrupoles: An Experiment Revisited." American Journal of Physics 67(8), 1999 pp. 660–664.