FindMinimum

FindMinimum[f,x]

searches for a local minimum in f, starting from an automatically selected point.

FindMinimum[f,{x,x0}]

searches for a local minimum in f, starting from the point x=x0.

FindMinimum[f,{{x,x0},{y,y0},…}]

searches for a local minimum in a function of several variables.

FindMinimum[{f,cons},{{x,x0},{y,y0},…}]

searches for a local minimum subject to the constraints cons.

FindMinimum[{f,cons},{x,y,…}]

starts from a point within the region defined by the constraints.

Details and Options

  • FindMinimum returns a list of the form {fmin,{x->xmin}}, where fmin is the minimum value of f found, and xmin is the value of x for which it is found.
  • If the starting point for a variable is given as a list, the values of the variable are taken to be lists with the same dimensions.
  • The constraints cons can contain equations, inequalities or logical combinations of these.
  • The constraints cons can be any logical combination of:
  • lhs==rhsequations
    lhs>rhs or lhs>=rhs inequalities
    {x,y,…}∈regregion specification
  • FindMinimum first localizes the values of all variables, then evaluates f with the variables being symbolic, and then repeatedly evaluates the result numerically.
  • FindMinimum has attribute HoldAll, and effectively uses Block to localize variables.
  • FindMinimum[f,{x,x0,x1}] searches for a local minimum in f using x0 and x1 as the first two values of x, avoiding the use of derivatives.
  • FindMinimum[f,{x,x0,xmin,xmax}] searches for a local minimum, stopping the search if x ever gets outside the range xmin to xmax.
  • Except when f and cons are both linear, the results found by FindMinimum may correspond only to local, but not global, minima.
  • By default, all variables are assumed to be real.
  • For linear f and cons, x∈Integers can be used to specify that a variable can take on only integer values.
  • The following options can be given:
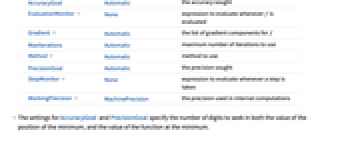
  • AccuracyGoalAutomaticthe accuracy sought
    EvaluationMonitor Noneexpression to evaluate whenever f is evaluated
    Gradient Automaticthe list of gradient components for f
    MaxIterationsAutomaticmaximum number of iterations to use
    Method Automaticmethod to use
    PrecisionGoalAutomaticthe precision sought
    StepMonitor Noneexpression to evaluate whenever a step is taken
    WorkingPrecision MachinePrecisionthe precision used in internal computations
  • The settings for AccuracyGoal and PrecisionGoal specify the number of digits to seek in both the value of the position of the minimum, and the value of the function at the minimum.
  • FindMinimum continues until either of the goals specified by AccuracyGoal or PrecisionGoal is achieved.
  • Possible settings for Method include "ConjugateGradient", "PrincipalAxis", "LevenbergMarquardt", "Newton", "QuasiNewton", "InteriorPoint", and "LinearProgramming", with the default being Automatic.

Examples

open allclose all

Basic Examples  (4)

Find a local minimum, starting the search at :

Extract the value of x at the local minimum:

Find a local minimum, starting at , subject to constraints :

Find the minimum of a linear function, subject to linear and integer constraints:

Find a minimum of a function over a geometric region:

Plot it:

Scope  (12)

With different starting points, you may get different local minima:

Local minimum of a two-variable function starting from x=2, y=2:

Local minimum constrained within a disk:

Starting point does not have to be provided:

For linear objective and constraints, integer constraints can be imposed:

Or constraints can be specified:

Find a minimum in a region:

Plot it:

Find the minimum distance between two regions:

Plot it:

Find the minimum such that the triangle and ellipse still intersect:

Plot it:

Find the disk of minimum radius that contains the given three points:

Plot it:

Using Circumsphere gives the same result directly:

Use to specify that is a vector in :

Find the minimum distance between two regions:

Plot it:

Options  (7)

AccuracyGoal & PrecisionGoal  (2)

This enforces convergence criteria and :

This enforces convergence criteria and :

Setting a high WorkingPrecision makes the process convergent:

EvaluationMonitor  (1)

Plot convergence to the local minimum:

Gradient  (1)

Use a given gradient; the Hessian is computed automatically:

Supply both gradient and Hessian:

Method  (1)

In this case, the default derivative-based methods have difficulties:

Direct search methods that do not require derivatives can be helpful in these cases:

NMinimize also uses a range of direct search methods:

StepMonitor  (1)

Steps taken by FindMinimum in finding the minimum of a function:

WorkingPrecision  (1)

Set the working precision to ; by default AccuracyGoal and PrecisionGoal are set to :

Applications  (3)

Annual returns (R) of long bonds from S&P 500 from 1973 to 1994:

Compute the mean and covariance from the returns:

Minimize the volatility subject to at least 10% return:

Find the smallest square that can contain circles of given radii for that do not overlap. Specify the number of circles and the radius of each circle:

If is the center of circle , then the objective is to minimize . The objective can be transformed so as to minimize and :

The circles must not overlap:

Collect the variables:

Minimize the objective :

The circles are contained in the square :

Compute the fraction of square covered by the circles:

Find a path through circular obstacles such that the distance between the start and end points is minimized:

The path is discretized into different points with distance of between points, where is the trajectory length being minimized:

The points cannot be inside the circular objects:

The start and end points are known:

Collect the variables:

Minimize the length subject to the constraints:

Visualize the result:

Properties & Relations  (2)

FindMinimum tries to find a local minimum; NMinimize attempts to find a global minimum:

Minimize finds a global minimum and can work in infinite precision:

FindMinimum gives both the value of the minimum and the minimizer point:

FindArgMin gives the location of the minimum:

FindMinValue gives the value at the minimum:

Possible Issues  (6)

With machine-precision arithmetic, even functions with smooth minima may seem bumpy:

Going beyond machine precision often avoids such problems:

If the constraint region is empty, the algorithm will not converge:

If the minimum value is not finite, the algorithm will not converge:

The integer linear programming algorithm is only available for machine-number problems:

Sometimes providing a suitable starting point can help the algorithm to converge:

It can be time-consuming to compute functions symbolically:

Restricting the function definition prevents symbolic evaluation:

Wolfram Research (1988), FindMinimum, Wolfram Language function, https://reference.wolfram.com/language/ref/FindMinimum.html (updated 2014).

Text

Wolfram Research (1988), FindMinimum, Wolfram Language function, https://reference.wolfram.com/language/ref/FindMinimum.html (updated 2014).

CMS

Wolfram Language. 1988. "FindMinimum." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/FindMinimum.html.

APA

Wolfram Language. (1988). FindMinimum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindMinimum.html

BibTeX

@misc{reference.wolfram_2024_findminimum, author="Wolfram Research", title="{FindMinimum}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FindMinimum.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findminimum, organization={Wolfram Research}, title={FindMinimum}, year={2014}, url={https://reference.wolfram.com/language/ref/FindMinimum.html}, note=[Accessed: 24-November-2024 ]}