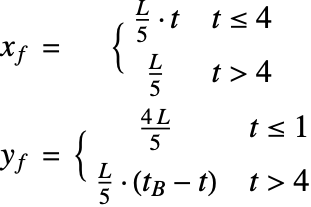Laser Beam Welding
| Introduction | Solve the PDE Model |
| Heat Transfer Model | Post-processing and Visualization |
| Domain | Nomenclature |
| Heat Source | References |
| Initial and Boundary Conditions |
Introduction
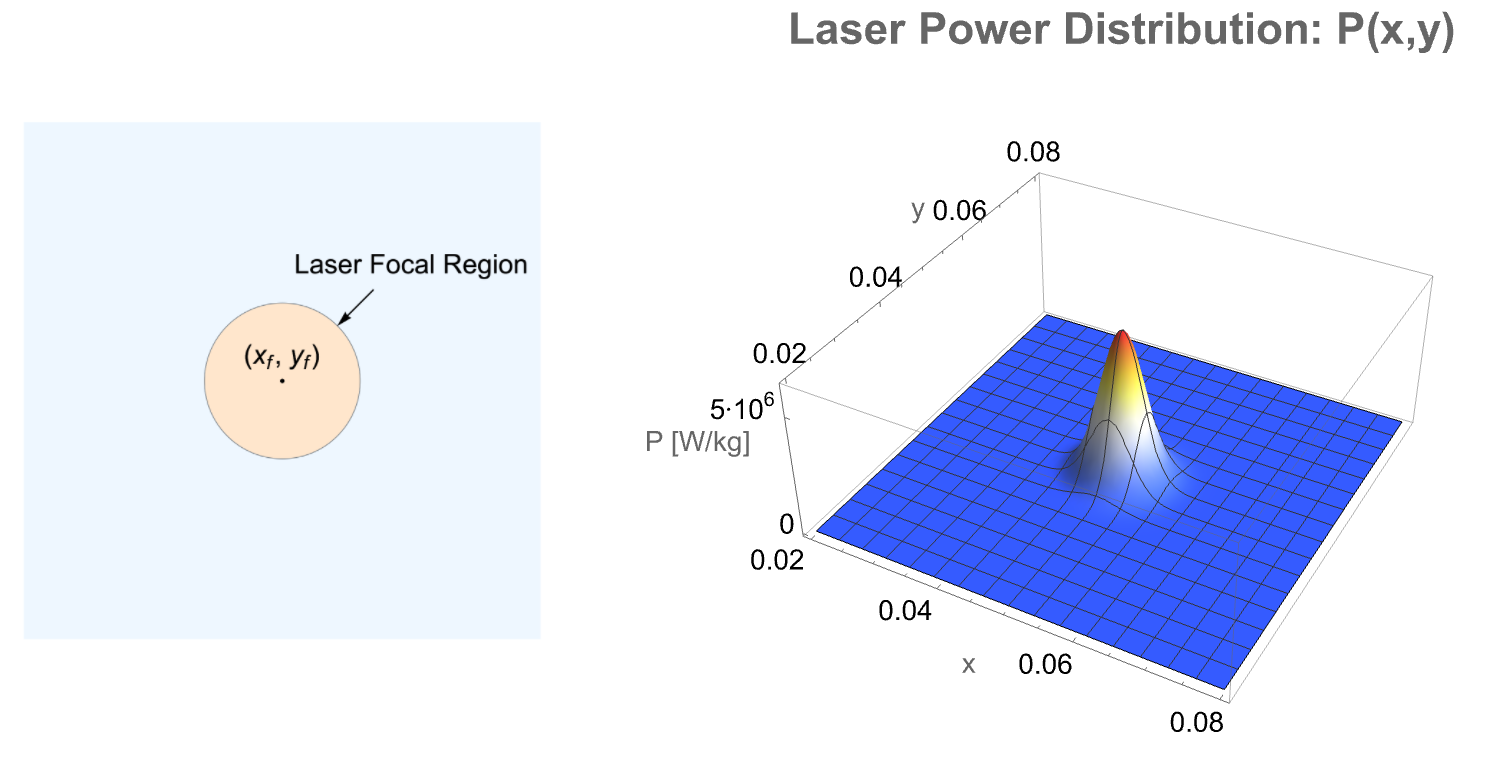
Laser beam welding (LBW) is a welding technique used to combine metals or thermoplastics. The laser beam provides concentrated, intense energy that heats up the materials at the welding location, and the parts melt together. In this example two pieces of steel are to be welded together horizontally to form a larger plate. A laser beam follows the edges to be welded and traverses the steel pieces for the time period of 
.
The evolution of the temperature field during the welding process is simulated with a heat transfer model. For a successful welding, the maximum temperature 
at each time step must be above the melting point of the material used, in this case of steel at 
.
Once the object is welded after 
heat continues to escapes through the objects' surfaces by radiation to the surrounding area, and the plate will cool down towards the ambient temperature 
. We can inspect the cooling process by calculating the time 
required to drop the plate temperature below a specific temperature 
.
The symbols and corresponding units used here are summarized in the Nomenclature section.
Please refer to the information provided in "Heat Transfer" for a more general theoretical background for heat transfer analysis.
Heat Transfer Model
The heat equation (1) is used to solve for the temperature field in a heat transfer model:
When modeling the heat transfer in a solid medium, there is no internal fluid flow that could cause a heat convection. Therefore the velocity term 
vanishes and the heat equation simplifies to
Since the internal convection introduced by the small amount of the melted steel is much weaker compared to the heat conduction that effect will be neglected in this model.
Domain
Two steel pieces will be welded together will form a larger plate with a length of 
, a width of 
and the thickness of 
.
In order to get a good result, a finer than the default grid is used for the mesh generation. Here we set the max edge length to be 
, which means that there will be at least one hundred elements in the 
(length) and 
(width) directions.
Heat Source
In this model the laser beam provides the thermal energy to weld the steel pieces, and is modeled by the heat source term 
in the heat equation (2). When applying the laser beam all particles within the focal region are irradiated and heated up simultaneously.
Assume the distribution of the laser power 
is described by a Gaussian bell shape at a focus point 
, and is homogeneous in the 
(thickness) direction. A parameter 
is introduced to control the degree of the laser concentration. A higher number implies a more concentrated beam.
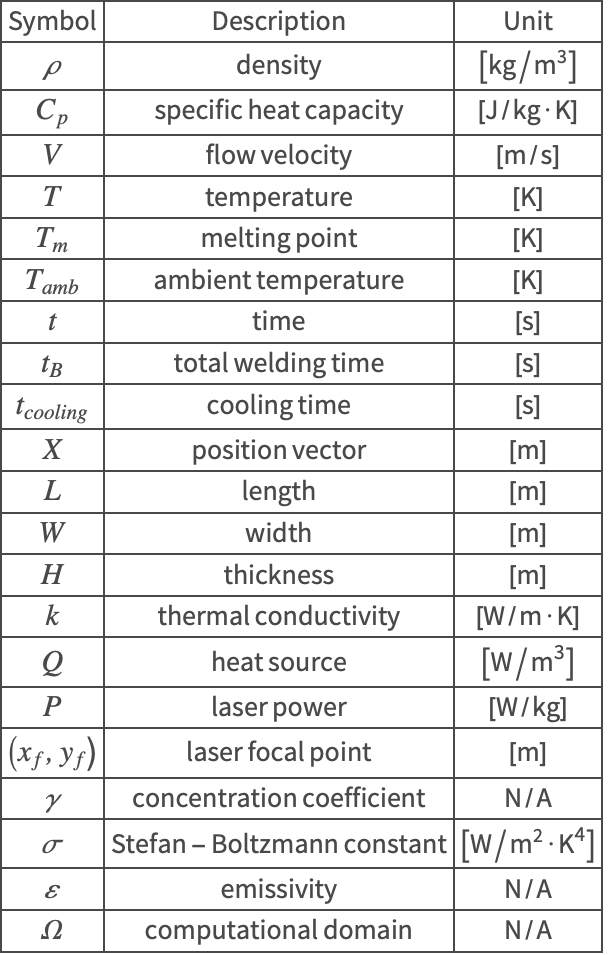
The laser beam is applied for a total time of 
. The path of the beam follows the edges to be welded, and is describe as a function of time 
:
Note, that all parameters except the independent variables are evaluated.
Initial and Boundary Conditions
At the beginning of the simulation, the temperature 
of the steel plate is assumed to be at the ambient temperature 
.
All the objects' surfaces are losing heat by radiation to the surrounding area. The Stefan-Boltzmann constant and the emissivity of steel are given by 
and 
, respectively.
Solve the PDE Model
Next we will solve the heat transfer PDE model with NDSolve.
Post-processing and Visualization
To inspect the effect of the laser welding, we visualize the temperature distribution 
evolving in time.
See this note about improving the visual quality of the animation.
Next, the maximum temperature 
is retrieved at each time step and compared with the melting point 
. Note that an effective welding requires 
during the welding process 
.
During the welding process: 
, the maximum temperature 
arises and exceeds the melting point 
, which confirms the effectiveness of the laser welding. For 
the joined steel plate gradually cools down by radiating to the surrounding, and drops below the melting point at 
.
Nomenclature
References
1. Abali B.E. Computational Reality: Solving Nonlinear and Coupled Problems in Continuum Mechanics. Advanced Structured Materials, vol 55. Springer, Singapore. (2017).