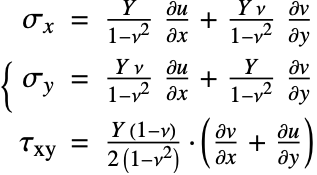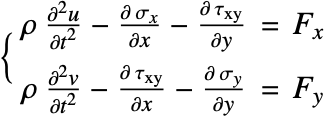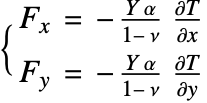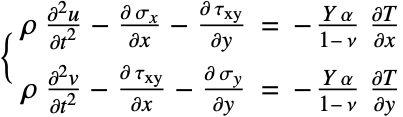Thermal Load on a Beam
| Introduction | Solve the PDE Model |
| Multiphysics Model | Post-processing and Visualization |
| Domain | Nomenclature |
Introduction
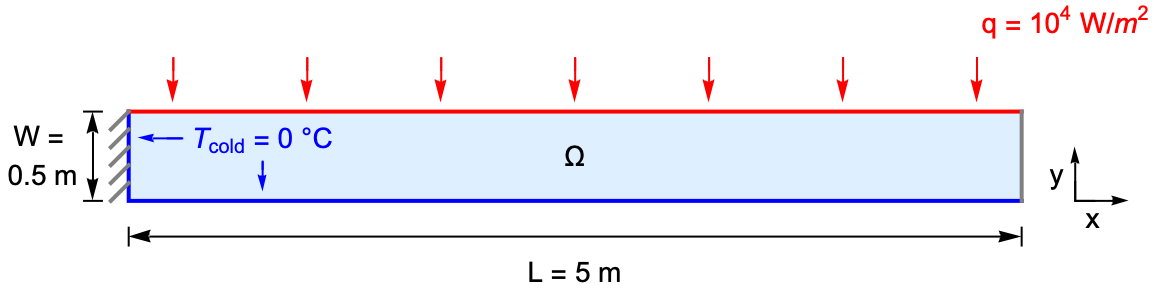
Thermal stress is a type of stress induced by a temperature change, which can lead to fracture or deformation of an object. In the following model, a steel beam is fixed at the left and heated by a constant inward heat flux ![]() on the top surface. The left and the lower surfaces are kept at
on the top surface. The left and the lower surfaces are kept at ![]() , while the right end is assumed to be thermally insulated.
, while the right end is assumed to be thermally insulated.
During the heating process the temperature on the top surface will be gradually increased. The resulting temperature gradient will then generate thermal stress and bend the beam downward.
The evolution of the temperature field and the thermally induced deformation are simulated by sequentially the heat transfer and the structural mechanics models. The location and values of horizontal and vertical displacement will then be calculated.
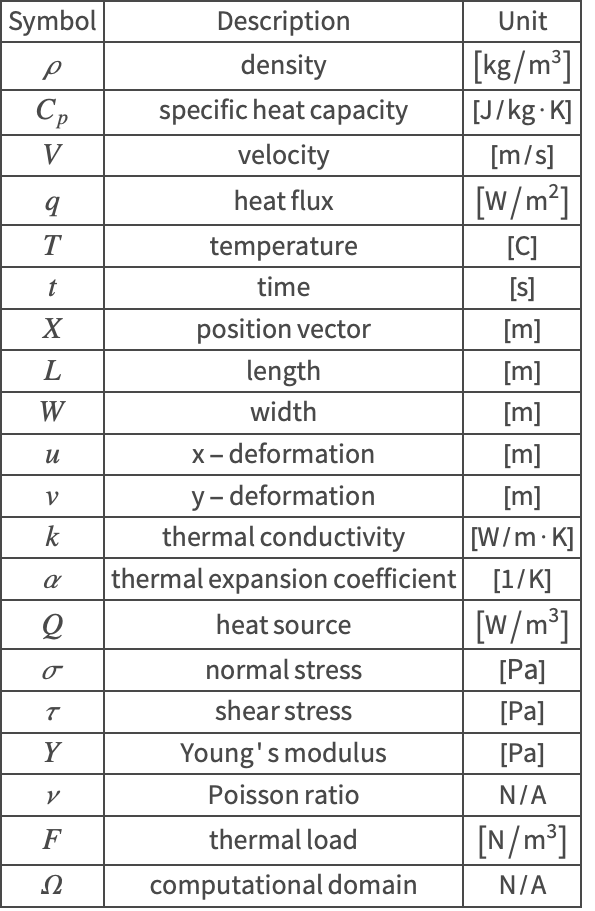
The symbols and corresponding units used here are summarized in the Nomenclature section.
Please refer to the information provided in "Heat Transfer" for a more general theoretical background for heat transfer analysis.
Multiphysics Model
There are two physical domains involved in this application: the heat transfer model and the structural mechanics model. The coupling between two models is one-way, since only the structural deformation depends on the temperature, but the temperature field does not depend on the deformation of the object in this model. This type of problem is considered as a sequential multiphysics model and will be solved in two steps.
First, the heat transfer model is built to simulate the temperature field ![]() of the beam. The structural mechanics model is then constructed and uses the temperature field previously computed to show the thermally induced deformation. This is what is called a sequential simulation and is possible because the deformation of the object does not couple back and influence the thermal distribution. Sequential models are possible when there is a coupling that is one directional. An alternative approach is to model both the temperature field and the deformation in a single PDE model. This is called a fully coupled model.
of the beam. The structural mechanics model is then constructed and uses the temperature field previously computed to show the thermally induced deformation. This is what is called a sequential simulation and is possible because the deformation of the object does not couple back and influence the thermal distribution. Sequential models are possible when there is a coupling that is one directional. An alternative approach is to model both the temperature field and the deformation in a single PDE model. This is called a fully coupled model.
In this approach, however, the heat equation is considered first and then the solid mechanics equation.
Heat Transfer Model
The heat equation (1) is used to solve for the temperature field in a heat transfer model:
For a transient heat transfer model without sources, the source term ![]() in (2) is set to zero. Since a solid is modeled, any internal velocity
in (2) is set to zero. Since a solid is modeled, any internal velocity ![]() also vanishes, and the heat equation simplifies to:
also vanishes, and the heat equation simplifies to:
Structural Mechanics Model
In structural mechanics, the plane stress relation (3) describes the deformation of thin objects. Here, "thin" means thin relative to the other dimensions of the object. The two dependent variables ![]() ,
, ![]() denote the deformation in the
denote the deformation in the ![]() and
and ![]() directions, respectively. As material data, Young's modulus
directions, respectively. As material data, Young's modulus ![]() and the Poisson ratio
and the Poisson ratio ![]() need to be specified.
need to be specified.
The equilibrium equation (4), which denotes the force balance in the ![]() and
and ![]() directions, is then used as the governing PDE of the structural mechanics model. On the right-hand side
directions, is then used as the governing PDE of the structural mechanics model. On the right-hand side ![]() and
and ![]() model any external force that may act on the object.
model any external force that may act on the object.
In this model, the temperature-induced thermal load is the only external force that applies on the beam and is coupled to the plane-stress PDE (5) as the source term on the right-hand side. The magnitude of the thermal load ![]() ,
, ![]() is related to the temperature
is related to the temperature ![]() and the thermal expansion coefficient
and the thermal expansion coefficient ![]() by the thermal stress equation.
by the thermal stress equation.
![]() is the density
is the density ![]() ,
,![]() is the heat capacity
is the heat capacity ![]() ,
,![]() is the thermal conductivity
is the thermal conductivity ![]() ,
,![]() is the Young's modulus
is the Young's modulus ![]() ,
,![]() is the thermal expansion coefficient
is the thermal expansion coefficient ![]() ,
,![]() is the Poisson ratio.
is the Poisson ratio.
Domain
The steel beam to be modeled has a length of ![]() and a width of
and a width of ![]() .
.
In order to get a good result, a grid finer than the default is applied for the mesh generation. Here the maximum grid size is set to ![]() so that about one thousand elements are used.
so that about one thousand elements are used.
Solve the PDE Model
In the following section, the heat transfer model will be solved first to simulate the temperature field ![]() of the beam. The structural mechanics model is then constructed to show the thermally induced deformation.
of the beam. The structural mechanics model is then constructed to show the thermally induced deformation.
Heat Transfer Model
At the beginning of the simulation, the temperature ![]() of the steel beam is set to the temperature
of the steel beam is set to the temperature ![]() .
.
The left and bottom surfaces are kept at the initial temperature ![]() at all times.
at all times.
The top surface of the beam is subjected to a constant inward heat flux ![]() .
.
To inspect the heat flow within the steel beam, the temperature distribution ![]() is visualized evolving in time.
is visualized evolving in time.
See this note about improving the visual quality of the animation.
Due to the inward heat flux ![]() on the top surface, the temperature difference across the beam has risen to
on the top surface, the temperature difference across the beam has risen to ![]() in less than three hours (
in less than three hours (![]() ).
).
With the temperature profile in hand, the corresponding thermal load on the beam can now be calculated. The beam deformation is solved by the structural mechanics model in the following section.
Structural Mechanics Model
In this model, the temperature-induced thermal load is the only external force that applies on the beam, and it is coupled to the plane-stress PDE (6) as the source term on the right-hand side. The magnitude of the thermal load ![]() ,
, ![]() is related to the temperature
is related to the temperature ![]() and the thermal expansion coefficient
and the thermal expansion coefficient ![]() by the thermal stress equation:
by the thermal stress equation:
On the left-hand side of the beam, the deformation variables ![]() ,
, ![]() are held fixed with zero displacement.
are held fixed with zero displacement.
To inspect the effect of the thermal loading, the following visualization combines the resulting structural deformation with the temperature field.
Post-processing and Visualization
In order to show the structural deformation, the deformed element mesh is created for the beam, based on the interpolating functions given.
Note that the deformation is scaled by a factor of ![]() to better demonstrate the result.
to better demonstrate the result.
See this note about improving the visual quality of the animation.
Next, to find the maximum beam deformation, the components ![]() ,
, ![]() are visualized with contour plots.
are visualized with contour plots.
In order to show the final deformation of the beam, the deformed element mesh and the resulting interpolating functions are set up at the simulation end time: ![]() .
.
It is seen that the largest deformation of the beam occurs at the upper-right corner. The maximum ![]() ,
, ![]() values can be retrieved to show the exact deformation amount in both the
values can be retrieved to show the exact deformation amount in both the ![]() and
and ![]() directions.
directions.
Under the thermal load, the steel beam has been stretched for around ![]() and been bent for
and been bent for ![]() .
.