The solid mechanics PDE components are in the experimental stage.

This notebook contains tests that verify that the solid mechanics partial differential equations (PDE) model works as expected. To run all tests, SelectAll and press Shift+Enter. The results will then be in the section Test Result Inspection.

Note that these tests can also serve as a basis for developing your own solid mechanics models. As such, the tests are grouped into stationary (time-independent) and transient (time-dependent) tests. In both categories, two- and three-dimensional tests can be found.

In each test case, the visualization section is there to provide post-processing results for inspection; however, it is not a necessary part of the test. In the interest of saving runtime and reducing memory consumption, the cells in the visualization section are set to not be evaluatable. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

The solid mechanics equations are used to solve for the displacement of a constrained object under load. Please refer to the information provided in "Solid Mechanics" for a more general theoretical background for solid mechanics analysis.

Stationary Tests

This section contains examples of stationary (non-time-dependent) solid mechanics PDE models for the validation.

2D Equations

This section contains examples of 2D stationary solid mechanics PDE models.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0001

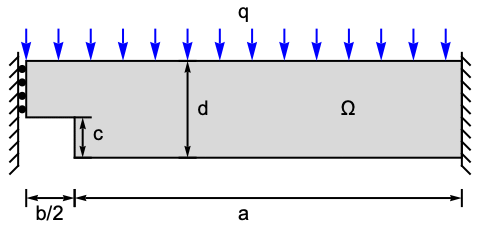
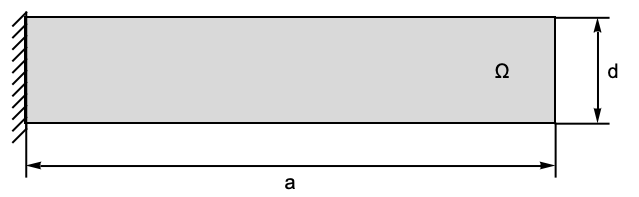
The following test cases verify various aspects of 2D plane stress analysis. The model domain is a notched beam with a total width of , a height of and thickness . At the left boundary, a roller constraint is present, and the structure is fixed at the right-hand side. A pressure of is acting in a downward direction on the top. The remaining boundaries are free to move. Young's modulus is given as and Poisson's ratio is .

M. Asghar Bhatti. Fundamental Finite Element Analysis and Applications. Wiley., p. 510, Example 7.7, Notched Beam.

M. Asghar Bhatti. Fundamental Finite Element Analysis and Applications. Wiley. Supplementary examples from book webpage, p. 34, Chapter 7, Notched Beam.

The standard plane stress model is used.

The nodal displacements are given.

The structure is held fixed at the right-hand side.

The structure is attached to a roller in the direction on the left.

On the top, a pressure of 50 units is applied in the downward direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

Bhatti's example goes further and computes various stresses. Bhatti's example exclusively is based on linear elements. In the Wolfram Language, however, a special technique is used to have a higher-order interpolation also in the linear element case and special algorithms to recover derivatives. Thus the stress values computed with the Wolfram Language and the simplistic (yet instructive) example of Bhatti do not match and are not shown here.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0002

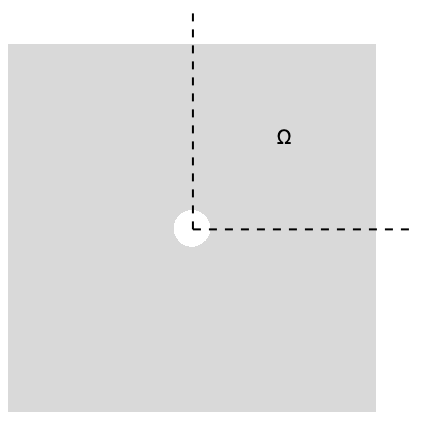
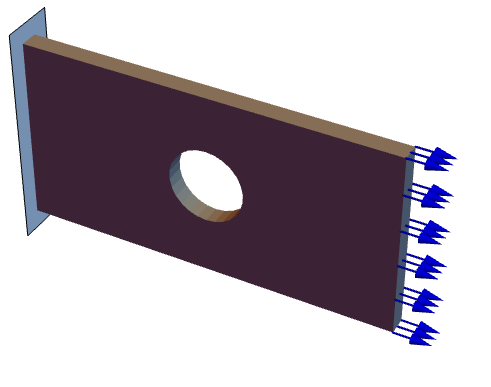
The following test case verifies 2D plane stress analysis and computes stresses to be compared with an analytical solution. The original model is for an infinite plate with a hole inside. To simulate this model, the domain is made finite and is a quarter-symmetry of the rectangular plate with a quarter-hole at the lower-left corner.

The modeled plate has a width of , a height of and thickness . The radius of the hole is . At the left boundary, a roller constraint is used such that the structure can move up or down but not to the right. At the bottom, there is a second roller constraint such that the structure can move left to right but not up and down. A pressure of is acting in the direction on the right-hand side. The remaining boundaries are free to move. Young's modulus is not needed and assumed as , and Poisson's ratio is .

D. Roylance, Mechanics of Materials, Wiley., p. 184.

The standard plane stress model is used.

An expression for the stress in the direction is given.

The structure is held fixed at the right-hand side.

The structure is attached to a roller in the y-direction on the left.

On the right, a pressure of 1000 [Pa] is applied in the downward positive direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

Aside from the expected deviation at the end, the analytical and simulated results match closely. The deviation at the end is expected because the analytical model is for an infinite plate that is not modeled here. Enlarging the domain by setting will further improve the quality of the solution.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0003

The following test case verifies a 2D plane stress analysis of a beam. The model domain is a beam with a total width of , a height of and thickness . At the left boundary, the beam is fixed to a wall. A pressure of is acting in a downward direction on the top. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is . The mass density is given as .

G. Backstrom, Simple Displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, p. 59.

The standard plane stress model is used.

The nodal displacements are given.

The structure is held fixed at the left-hand side.

On the top, a pressure of 10^6 units is applied in the downward direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

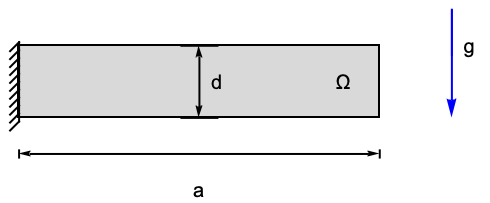
SolidMechanics-FEM-Stationary-2D-PlaneStress-0004

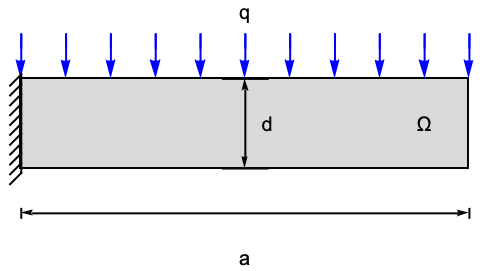
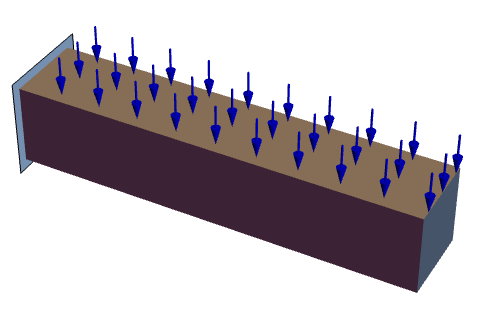
The following test case verifies a 2D plane stress analysis of a beam. The model domain is a beam with a total width of , a height of and thickness . At the left boundary, the beam is fixed to a wall. The remaining boundaries are free to move. Gravity acts on the body. Young's modulus is given as , and Poisson's ratio is . The mass density is given as .

G. Backstrom, Simple displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, Page 68

The standard plane stress model is used.

The nodal displacements are given.

The structure is held fixed at the left hand side.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save the runtime and consume memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0005

The model domain is a beam with a total length of , a height of and thickness . At the right boundary the beam is fixed to a wall. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is , which makes this compatible with beam theory. The maximal bending stress at the middle of the beam ( and the fixed end ( are sought.

S. H. Crandall and N. C. Dahl, An Introduction to the Mechanics of Solids, McGraw-Hill Book Co., Inc., New York, NY, 1959, p. 342, problem 7.18.

The standard stress model with a thickness specified is used.

The maximum bending stress at mid-length and the fixed end are sought.

The beam is fixed at the right-hand side.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0006

The model domain is a beam with a total length of , a height of and thickness . At the left boundary, the beam is fixed to a wall. At the right, there are two load test cases: case 1 is a bending moment and case 2 is an upward force. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is . For each test case, the deflection at the free and is sought as well as the bending stress at a distance from the fixation at the left.

R. J. Roark, Formulas for Stress and Strain, 4th ed., McGraw-Hill Book Co., Inc., New York, NY, 1965, pp. 104, 106.

The standard stress model is used.

Reference values are given.

The beam is fixed at the left-hand side.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

SolidMechanics-FEM-Stationary-2D-PlaneStress-0007

A rectangular plate is fixed at the bottom. Three boundary loads are applied on the left, top and right such that the normal strains vanish and the shear strain is constant.

G. Backstrom, Simple Displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, p. 56.

The standard plane stress model is used.

Reference values are given.

The plate is fixed at the bottom, and pressures or forces are applied at the remaining boundaries.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

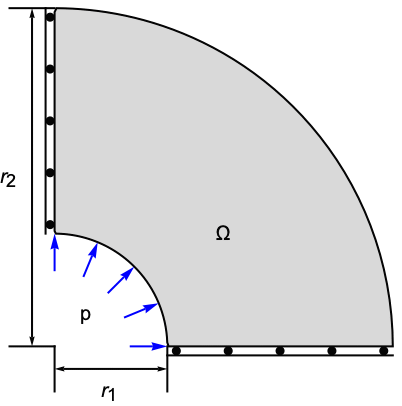
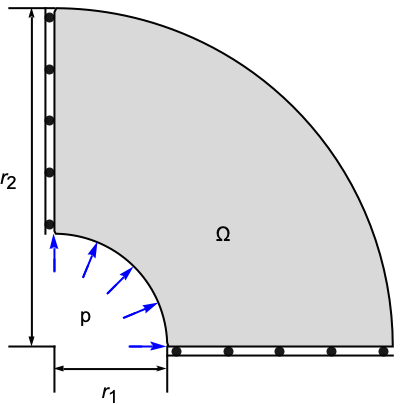
SolidMechanics-FEM-Stationary-2D-PlaneStrain-0001

The following test cases verify various aspects of 2D plane strain analysis. The model domain is a quarter–cross section through a pipe with an inner radius , an outer radius and a thickness . At the left boundary, a symmetry constraint is used such that the pipe can move up and down, and at the right bottom, a second symmetry constraint is used such that the pipe can move left and right. A pressure of is acting within the pipe. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is .

M. Asghar Bhatti, Fundamental Finite Element Analysis and Applications. Wiley, p. 517, Example 7.9, Pressure Vessels.

The standard plane strain model is used.

The tangential and radial stresses are given.

The quarter-pipe structure exploits a symmetry condition in direction on the left.

Inside, a pressure of 20 units is applied in the outward direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure Evaluatable is ticked.

3D Equations

This section contains examples of 3D stationary solid mechanics PDE models.

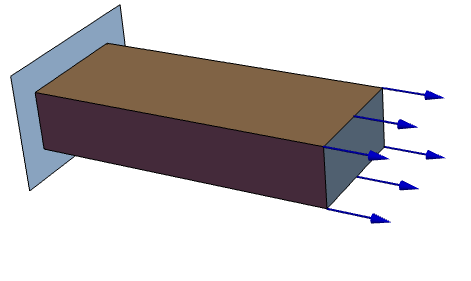
SolidMechanics-FEM-Stationary-3D-0001

The following test cases verify a 3D stress analysis. The model domain is a beam with a length of , a width of and a height of . At the left boundary, the beam is fixed to a wall. At the right-hand side, a force of is acting in the direction. The remaining boundaries are free to move. As a material, a S235 steel is used. Thus Young's modulus is given as , and Poisson's ratio is .

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, p. 7.

The standard stress model is used.

An expected elongation in the direction of is given. Inside the domain, a stress of is given. The elongation can be computed with

It follows that

The stress in is computed to be

The structure is held fixed at the left-hand side.

On the right-hand side, a force of acts in the direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

SolidMechanics-FEM-Stationary-3D-0002

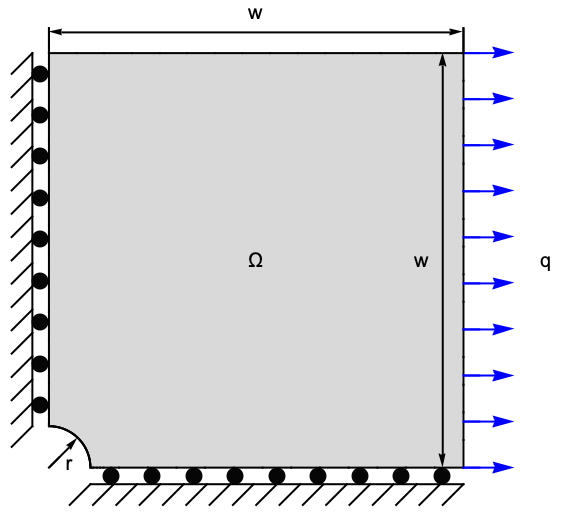
The following test cases verify a 3D stress analysis. The model domain is a perforated plate with a length of , a width of and a height of . The perforation is at the center and has a diameter of . At the left boundary, the plate is fixed to a wall. At the right-hand side, a force of is acting in the direction. The remaining boundaries are free to move. As a material, a S235 steel is used. Thus Young's modulus is given as , and Poisson's ratio is .

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, p. 13.

The standard stress model is used.

An expected maximum von Mises stress of is given.

The analytical estimation of the von Mises stress is given by

where is stress concentration factor from a lookup table. In this case, the aspect ratio of the radius of the diameter and half the plate's height result in

The nominal stress on the - cross section through the perforation is computed to be

The expected maximal stress is then

The structure is held fixed at the left-hand side.

On the right-hand side, a force of acts in the direction.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

SolidMechanics-FEM-Stationary-3D-0003

The following test cases verify an applied boundary load. The model domain is a beam with a length of , a width of and a height of . At the left boundary, the plate is fixed to a wall. At the right-hand side, a force of is acting in the negative direction. The remaining boundaries are free to move. As a material, a S275 steel is used. Thus Young's modulus is given as , and Poisson's ratio is .

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, p. 29.

The standard stress model is used.

An expected maximum displacement in the negative direction of is given.

The analytical estimation of the maximum deflection in the direction is given by

where the moment . is the applied force and the length of the beam.

The structure is held fixed at the left-hand side.

On the right-hand side, a force of acts in the negative direction.

The remaining sides are free to move.

The example goes further and computes a normal stress at the fixation of the beam and the wall. The numerical value deviates from the analytical solution because of stress singularities. In the given reference, a somewhat arbitrary point is chosen for the comparison of the analytical stress value with the numerically computed value close to the singularity. This approach does not seem optimal, so this test will be skipped.

SolidMechanics-FEM-Stationary-3D-0004

The following test cases verify a distributed load. The model domain is a beam with a length of , a width of and a height of . At the left boundary, the beam is fixed to a wall. On the top face, a load of is applied and acting in the negative direction. Note the units of force per length. The remaining boundaries are free to move. As a material, a S275 steel is used. Thus Young's modulus is given as , and Poisson's ratio is .

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, p. 32.

The standard stress model is used. Note that the material parameters are given in the scale of millimeters .

An expected maximum displacement in the negative direction of is given.

The analytical estimation of the maximum deflection in the direction is given by

where the moment . is the applied distributed force and the length of the beam.

The structure is held fixed at the left-hand side.

On the top side, a distributed force of acts in the negative direction. Since the length of the beam is , the total force acting is .

The remaining sides are free to move.

The example goes further and computes a normal stress at the fixation of the beam and the wall. The numerical value deviates from the analytical solution because of stress singularities. In the given reference, a somewhat arbitrary point is chosen for the comparison of the analytical stress value with the numerically computed value close to the singularity. This approach does not seem optimal, so this test will be skipped.

SolidMechanics-FEM-Stationary-3D-0005

The following test cases verify a torque boundary load. The model domain is a rod with a length of and a diameter of . At the left boundary, the rod is fixed to a wall. At the right end, a moment of is applied. The remaining boundaries are free to move. As a material, a S275 steel is used. Thus Young's modulus is given as , and Poisson's ratio is .

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, p. 35.

The standard stress model is used.

The structure is held fixed at the left-hand side.

On the right-hand side, a torque of is present. This torque needs to be converted into a surface pressure. Start from

where is the shear stress (a pressure), the radius and the second moment of area [m^4]. After rearranging:

The remaining sides are free to move.

SolidMechanics-FEM-Stationary-3D-0006

A tapered aluminium alloy bar of square cross section and length is fixed to the ground. An axial load is applied to the free end of the bar.

C. O. Harris, Introduction to Stress Analysis, The Macmillan Co., New York, NY, 1959, pg. 237, problem 4.

The standard stress model is used.

The bar is fixed at the bottom.

Eigenmode Analysis Tests

2D Equations

This section contains examples of 2D eigenmode solid mechanics PDE analysis.

SolidMechanics-FEM-Stationary-2D-Eigenmode-0001

The following test case verifies a 2D plane stress analysis of a beam. The model domain is a beam with a total length of , a height of and thickness . At the left boundary, the beam is fixed to a wall. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is . The mass density is given as .

None

The standard stress model is used.

The expected natural frequencies be computed with:

Here is Youngs modulus, the height, the width, the mass density, the beam length and is:

It follows that

The beam is fixed at the left-hand side.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

3D Equations

This section contains examples of 3D eigenmode solid mechanics PDE analysis.

SolidMechanics-FEM-Eigenmode-3D-0001

The following test cases verify a 3D eigenmode analysis. The model domain is a beam with a length of , a width of and a height of . At the left boundary, the beam is fixed to a wall. The remaining boundaries are free to move. Young's modulus is given as , and Poisson's ratio is . The mass density is .

None

The standard stress model is used.

The expected natural frequencies be computed with:

Here is Youngs modulus, the moment of inertia, the mass density, the area of the cross section and the beam length. The is a factor dependent on the vibration mode and given as .

It follows that

The structure is held fixed at the left-hand side.

The remaining sides are free to move.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

SolidMechanics-FEM-Eigenmode-3D-0002

The following test cases verify a 3D eigenmode analysis. The model domain is a cylinder with a height of , an internal radius of and an external radius of . The cylinder is free to move. Young's modulus is given as , and Poisson's ratio is . The mass density is .

F. Abassian, D. J. Dawswell and N.C. Knowles, Free Vibration Benchmarks, vol.3, NAFEMS, Glasgow, 1987.

The standard stress model is used.

The expected natural frequencies can be computed with:

Here is the mass density, the cylinder height and the Shear modulus:

Here is the Young’s modulus and is the Poisson ratio.

It follows that:

The cylinder is unconstrained and free to move.

Next, the various PDE models are solved over the different meshes.

The following cells are marked as not evaluatable to save runtime and consumed memory. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

Test Result Inspection

This section contains the evaluation of the test runs. It works by collecting all instances of TestResultObject and generating a TestReport.

If the preceding table is empty, all tests succeeded.

Related Tech Notes

▪
• PDEModels Overview