PrimalityProving`
PrimalityProving`
PrimeQCertificate
gives a certificate that n is prime or that n is composite.
Details and Options
- To use PrimeQCertificate, you first need to load the Primality Proving Package using Needs["PrimalityProving`"].
- PrimeQCertificate uses the Pratt certificate and the Atkin–Morain certificate for primality.
- A certificate of compositeness is a list of three integers, either {a,n-1,n} or {a,2,n}, with
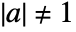. - A prime
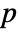always satisfies 
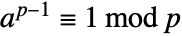. The certificate {a,n-1,n} can be used to show that n is composite by demonstrating that 
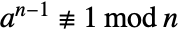. - Any number
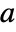whose square is 
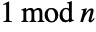for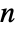 
prime must satisfy 
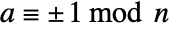. The certificate {a,2,n} can be used to show that n is composite by demonstrating that 
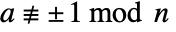and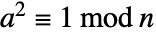 
. - A certificate of primality consists of a recursive list of certificates which prove that
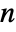is a prime if one or more smaller numbers are prime as well. - PrimeQCertificate has the same options as ProvablePrimeQ.
Examples
Basic Examples (2)
A certificate that can be used to prove that 1093 is a prime:
The same certificate can be obtained by using ProvablePrimeQ with the option "Certificate"->True:
A certificate that can be used to prove that 1093×3511 is composite:
The output is a list of three integers that indicate 1093×3511 is composite, and that it violates Fermat's little theorem for primes, 
if 
is prime: