Splines`
Splines`

SplineFit

バージョン7.0現在で，スプラインパッケージの機能のいくつかがWolfram言語カーネルに組み込まれている． »

SplineFit[{pt1,pt2,…},type]

点 pt1,pt2,…から指定された type のSplineFunctionオブジェクトを生成する．

詳細とオプション

  • SplineFitを使うためには，まずスプラインパッケージ をロードしなくてはならない．それにはNeeds["Splines`"]を実行する必要がある．
  • SplineFunctionオブジェクトは，引数0が pt1に，1が pt2に，のように順に対応するような点 pt1,pt2,…により指定された曲線をパラメータ化する関数である．
  • サポートされるタイプはCubic，Bezier，CompositeBezierである．
  • 三次スプラインは 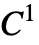C^(1)連続の区分的な三次多項式から構成され，それが生成されたそれぞれの点を補間する．端点におけるスプラインの二次導関数は0に設定される．
  • ベジエスプラインは端点のみを補間する．その他の点がスプラインを制御し凸包を形成する．n 個の点が与えられると，次数 n–1のスプラインが生成される．
  • 合成ベジエスプラインは 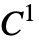C^(1)連続の三次ベジエ曲線連続で構成される．これは補間する点と制御点が交互になっている．
  • 偶数個の点から生成された合成ベジエスプラインでは，最終の点が補間点で，最後から2番目の点が最終部分の制御点となるよう，最後の2点が入れ替わる．奇数個の場合は，最後の頂点が2倍になる．
  • 点 pt1,pt2,…は二次元に限定されない．

例題

例  (1)

SplineFitは適切なタイプのSplineFunctionを返す：

3種類のスプラインをランダムな5つの点の集合にフィットする：

結果のスプラインをプロットする：

SplineFitは任意の次元で使える：

Wolfram Research (2008), SplineFit, Wolfram言語関数， https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

テキスト

Wolfram Research (2008), SplineFit, Wolfram言語関数， https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

CMS

Wolfram Language. 2008. "SplineFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

APA

Wolfram Language. (2008). SplineFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/Splines/ref/SplineFit.html

BibTeX

@misc{reference.wolfram_2024_splinefit, author="Wolfram Research", title="{SplineFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/Splines/ref/SplineFit.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_splinefit, organization={Wolfram Research}, title={SplineFit}, year={2008}, url={https://reference.wolfram.com/language/Splines/ref/SplineFit.html}, note=[Accessed: 22-November-2024 ]}