WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

Accuracy
✖
Accuracy

Accuracy[x]

给出数 x 小数点右侧的有效位数.

更多信息

范例

打开所有单元关闭所有单元

基本范例  (3)常见实例总结

机器精度数：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-gv36x
Out[1]=1

任意精度数：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-ctnrxg
Out[1]=1

精确数：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-1ry4x
Out[1]=1

范围  (4)标准用法实例范围调查

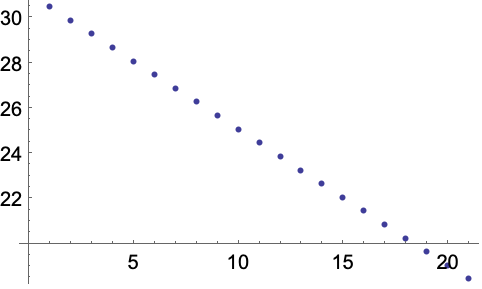
Accuracy 显示为小数点右侧已知的有效位数：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-nh7ue9
Out[1]=1

已知准确度为20的零：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-xrbov
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-c12cvu
Out[2]=2

z+1 的精确度与 z 的准确度相同：

In[3]:=3
✖
https://wolfram.com/xid/0bn6phu-fj761e
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bn6phu-bzvkpz
Out[4]=4

一个机器零的准确度：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-j5f8rx
Out[1]=1

0. 的不确定性等于最小的正的规范化机器数的不确定性：

In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-2o69qb
Out[2]=2

指定准确度作为 N 的目标：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-lbje9r
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-7rzxw
Out[2]=2

推广和延伸  (1)推广和延伸使用的实例

一个符号表达式的准确度是其数值准确度的极小值:

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-bxersu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-kjkj3y
Out[2]=2

应用  (2)用该函数可以解决的问题范例

检查一个结果的质量：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-cpvuay
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-u9ebq
Out[2]=2

跟踪一个重复计算的准确度损失：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-hsz4o
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-fywbqm
Out[2]=2

属性和关系  (4)函数的属性及与其他函数的关联

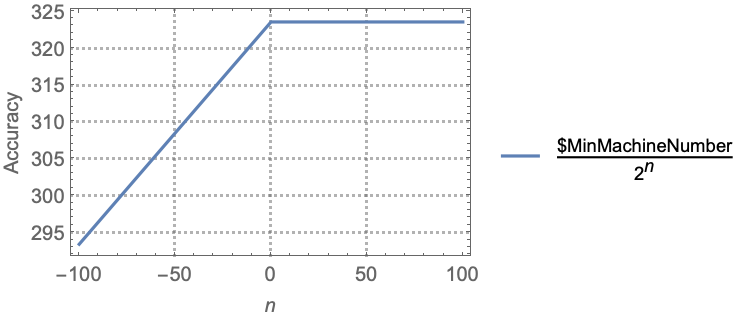
对于规范化的机器精度数，Accuracy[x] 与 $MachinePrecision-Log[10,Abs[x]] 相同：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-dvglfa
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-gopa7c
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bn6phu-c87pq5
Out[3]=3

没有机器数的准确度能高于 $MinMachineNumber：

In[4]:=4
✖
https://wolfram.com/xid/0bn6phu-h5wbhd
Out[4]=4

复数的实部和虚部可以有不同的精确度：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-cob2w2
Out[1]=1

算术运算通常会将其一起运算：

In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-8kqjz
Out[2]=2

但要注意的是，实部和虚部的精度可能仍然不同：

In[3]:=3
✖
https://wolfram.com/xid/0bn6phu-zlrrjh
Out[3]=3

整个数字的精确度总是小于或等于这两个精确度中的任何一个：

In[4]:=4
✖
https://wolfram.com/xid/0bn6phu-3z5xyg
Out[4]=4

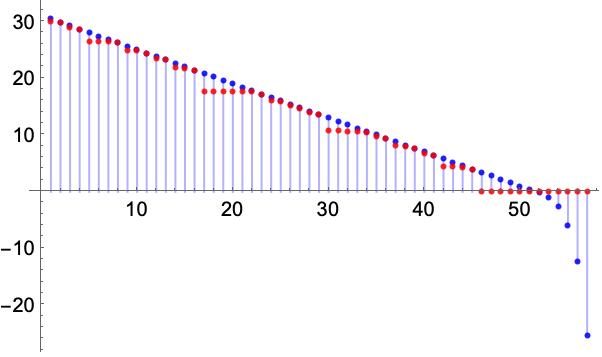
对于机器数，大小变小时准确度增加，$MinMachineNumber 的准确度最大：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-fy6ujt
Out[1]=1

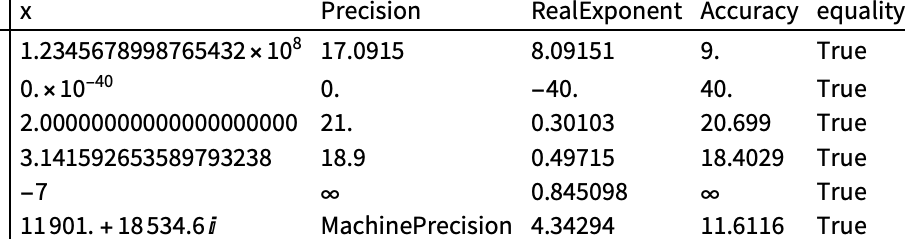
对于近似数，Precision[x]==RealExponent[x]+Accuracy[x]：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-e0pa5i
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-5jcx2p

可能存在的问题  (1)常见隐患和异常行为

非规范机器数不满足关系式 Precision[x]==RealExponent[x]+Accuracy[x]：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-fbf2yt
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-599rkn
Out[2]=2

相反，所有非规范数具有与 $MinMachineNumber 相同的不确定性：

In[3]:=3
✖
https://wolfram.com/xid/0bn6phu-ja1q3k
Out[3]=3

巧妙范例  (1)奇妙或有趣的实例

Accuracy 和 Precision 在逻辑图迭代中：

In[1]:=1
✖
https://wolfram.com/xid/0bn6phu-bubj5h
In[2]:=2
✖
https://wolfram.com/xid/0bn6phu-iwygwj
In[3]:=3
✖
https://wolfram.com/xid/0bn6phu-d41s53
Out[3]=3
Wolfram Research (1988)，Accuracy，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Accuracy.html （更新于 2018 年）.
✖
Wolfram Research (1988)，Accuracy，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Accuracy.html （更新于 2018 年）.

文本

Wolfram Research (1988)，Accuracy，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Accuracy.html （更新于 2018 年）.

✖
Wolfram Research (1988)，Accuracy，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Accuracy.html （更新于 2018 年）.

CMS

Wolfram 语言. 1988. "Accuracy." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2018. https://reference.wolfram.com/language/ref/Accuracy.html.

✖
Wolfram 语言. 1988. "Accuracy." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2018. https://reference.wolfram.com/language/ref/Accuracy.html.

APA

Wolfram 语言. (1988). Accuracy. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Accuracy.html 年

✖
Wolfram 语言. (1988). Accuracy. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Accuracy.html 年

BibTeX

@misc{reference.wolfram_2025_accuracy, author="Wolfram Research", title="{Accuracy}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/Accuracy.html}", note=[Accessed: 14-April-2025 ]}

✖
@misc{reference.wolfram_2025_accuracy, author="Wolfram Research", title="{Accuracy}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/Accuracy.html}", note=[Accessed: 14-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_accuracy, organization={Wolfram Research}, title={Accuracy}, year={2018}, url={https://reference.wolfram.com/language/ref/Accuracy.html}, note=[Accessed: 14-April-2025 ]}

✖
@online{reference.wolfram_2025_accuracy, organization={Wolfram Research}, title={Accuracy}, year={2018}, url={https://reference.wolfram.com/language/ref/Accuracy.html}, note=[Accessed: 14-April-2025 ]}