Adjugate

Adjugate[m]

给出方阵 m 的伴随矩阵.

更多信息

  • 伴随矩阵也称为伴随阵，其英文称为 adjugate matrix、classical adjoint matrix 或 adjunct matrix.
  • 可逆矩阵 m 的伴随矩阵由 Inverse[m]Det[m] 给出.
  • 矩阵 m 与其伴随矩阵的矩阵乘积等于 m 的行列式乘以与 m 相同大小的单位矩阵.
  • 矩阵 m 可以是数字或符号，但必须是方阵.

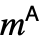范例

打开所有单元关闭所有单元

基本范例  (3)

计算 2×2 矩阵的伴随矩阵：

计算符号矩阵的伴随矩阵：

计算 3×3 矩阵的伴随矩阵：

验证与 m 的关系：

范围  (9)

基本用法  (5)

机器精度矩阵的伴随矩阵：

复矩阵的伴随矩阵：

为精确矩阵计算伴随矩阵：

为任意精度矩阵计算伴随矩阵：

符号矩阵的伴随矩阵：

特殊矩阵  (4)

稀疏矩阵的伴随以正规矩阵的形式返回：

结构化矩阵的伴随矩阵：

单位矩阵的伴随矩阵为其自身：

希尔伯特矩阵的伴随矩阵：

应用  (4)

使用 Adjugate 计算共同因子：

验证函数 cofactor：

使用 Adjugate 计算矩阵的逆：

与 Inverse 比较：

使用 Adjugate 求解线性方程：

与 LinearSolve 比较：

定义一个函数用于计算以隐式笛卡尔坐标方程表示的曲面的高斯曲率：

具有二十面体对称性的曲面的隐性笛卡尔方程：

计算其高斯曲率：

可视化曲面上的正（红色）和负（蓝色）高斯曲率区域：

属性和关系  (5)

m.Adjugate[m] 等于 Det[m] 乘以与其尺寸相同的单位矩阵：

Inverse[m] 等于伴随矩阵除以行列式：

对于 n×n 矩阵 m，Adjugate[m] 等于 LinearSolve[m,Det[m]IdentityMatrix[n]]：

对于 n×n 矩阵 m，Det[Adjugate[m]]==Det[m]n-1：

Minors[m] 可使用 Adjugate 进行计算：

可能存在的问题  (1)

伴随矩阵仅针对方阵有定义：

巧妙范例  (2)

定义一个函数来计算方阵的伴随多项式：

计算矩阵的伴随多项式：

对矩阵自身计算伴随多项式将得到伴随矩阵：

定义一个函数来计算方阵的迭代伴随矩阵：

计算矩阵的前几次迭代：

这等价于使用 NestList 与 Adjugate:

Wolfram Research (2021)，Adjugate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Adjugate.html.

文本

Wolfram Research (2021)，Adjugate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Adjugate.html.

CMS

Wolfram 语言. 2021. "Adjugate." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Adjugate.html.

APA

Wolfram 语言. (2021). Adjugate. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Adjugate.html 年

BibTeX

@misc{reference.wolfram_2024_adjugate, author="Wolfram Research", title="{Adjugate}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Adjugate.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_adjugate, organization={Wolfram Research}, title={Adjugate}, year={2021}, url={https://reference.wolfram.com/language/ref/Adjugate.html}, note=[Accessed: 18-November-2024 ]}