

Minors
Details

- For an
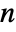 ×
×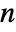 matrix the
matrix the 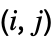
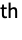 element of Minors[m] gives the determinant of the matrix obtained by deleting the
element of Minors[m] gives the determinant of the matrix obtained by deleting the 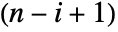
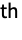 row and the
row and the 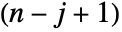
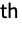 column of m. »
column of m. » - Reverse[Minors[m],{1,2}] makes the
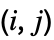
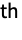 element correspond to deleting the
element correspond to deleting the 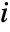
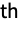 row and
row and 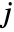
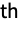 column of m. »
column of m. » - Minors[m] is equivalent to Minors[m,Min[Dimensions[m]]-1]. »
- Minors[m,k] gives the determinants of the k×k submatrices obtained by picking each possible set of k rows and k columns from m.
- Each element in the result corresponds to taking rows and columns with particular lists of positions. The ordering of the elements is such that reading across or down the final matrix, the successive lists of positions appear in lexicographic order.
- For an
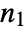 ×
×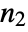 matrix, Minors[m,k] gives an
matrix, Minors[m,k] gives an 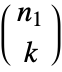 ×
×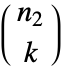 matrix.
matrix.
Examples
open all close allScope (14)
Basic Uses (6)
Specifying the Minors Size (4)
The matrices used to compute the minors:
The dimensions of Minors[m,k] for the allowed values of k for a 4×4 matrix:
Though Minors[m,0] and Minors[m,4] have the same dimensions, they are different matrices:
Note that Minors[m,4] equals {{Det[m]}}:
Similarly, Minors[m,1] and Minors[m,3] are different matrices:
Note that Minors[m,3] equals Minors[m]:
Minors[m,2] has the largest dimensions:
The matrices used to compute the minors:
The dimensions of Minors[m,k] for the allowed values of k for a 3×4 matrix:
Special Matrices (4)
Minors of structured matrices:
IdentityMatrix[n] is not changed by Minors:
For different values of k, it gives an identity matrix of the appropriate size:
Minors of HilbertMatrix:
Applications (5)
Visualize the determinants used to compute Minors[m] for a square matrix:
Reverse both levels of m to get the ![]()
![]() entry to come from deleting the
entry to come from deleting the ![]()
![]() row and
row and ![]()
![]() column:
column:
The adjugate matrix is its transpose:
Compare with the result returned by Adjugate:
The rank is the largest k for which Minors[mat,k] contains nonzero entries:
Use MatrixRank to check that the rank is indeed equal to two:
Test if a Hermitian matrix is positive definite using Sylvester's criterion:
Since all of the leading principle minors are positive, the matrix is positive definite:
Confirm the result using PositiveDefiniteMatrixQ:
Find the singularities of an algebraic space curve:
Properties & Relations (11)
For an ![]() matrix, Minors[m] is the matrix of determinants found by deleting row
matrix, Minors[m] is the matrix of determinants found by deleting row ![]() and column
and column ![]() :
:
Reverse[Minors[m],{1,2}] is the matrix of determinants found by deleting the ![]()
![]() row and
row and ![]()
![]() column of m:
column of m:
For an ![]() matrix and a fixed
matrix and a fixed ![]() from 1 to
from 1 to ![]() ,
, ![]() :
:
With r=Reverse[Minors[m],{1,2}], this can be expressed as ![]() :
:
The transposed equality ![]() also holds:
also holds:
Minors[m] is equivalent to Minors[m]==Minors[m,Min[Dimensions[m]]-1]:
For a square matrix m, Minors[m,Length[m]] equals {{Det[m]}}:
By definition, Minors[m,0] is {{1}}:
Minors of dimension higher than the MatrixRank are zero:
The Dimensions of the ![]()
![]() minors of an
minors of an ![]() ×
×![]() matrix are
matrix are ![]() ×
×![]() :
:
Minors of a square identity matrix is another identity matrix:
This is not true of rectangular identity matrices:
Minors of a square diagonal matrix is another diagonal matrix:
Minors is effectively equivalent to an outer product of row and column extractions:
Tech Notes
Related Guides
History
Introduced in 1988 (1.0) | Updated in 1999 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2) ▪ 2022 (13.1)
Text
Wolfram Research (1988), Minors, Wolfram Language function, https://reference.wolfram.com/language/ref/Minors.html (updated 2022).
CMS
Wolfram Language. 1988. "Minors." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Minors.html.
APA
Wolfram Language. (1988). Minors. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Minors.html
BibTeX
@misc{reference.wolfram_2025_minors, author="Wolfram Research", title="{Minors}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Minors.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_minors, organization={Wolfram Research}, title={Minors}, year={2022}, url={https://reference.wolfram.com/language/ref/Minors.html}, note=[Accessed: 11-March-2026]}