ArrayReduce

ArrayReduce[f,array,n]

f を適用することで array の次元 n を削減する．

ArrayReduce[f,array,n1;;n2]

次元 n1から n2を削減する．

ArrayReduce[f,array,{n1,n2,…}]

次元 n1，n2等を削減する．

ArrayReduce[f,array,{{n11,n12,…},{n21,n22,…},…}]

すべての次元 nijを組み合せて形成された配列に f を適用して各次元を i にする．

詳細

  • 配列の削減は配列の集約とも呼ばれるもので，配列の特定の次元に沿って，Mean，Total，StandardDeviation等の関数の計算に使われる．
  • ArrayReduce[f,array,n]の f は配列の第 n 次元に沿ったすべてのベクトルに適用される．これは，次元 n が最終次元になり，その後に低レベルのベクトルに f が適用される転置と見ることができる．
  • array の次元が{d1,d2,…}で関数がベクトルをスカラーに変換するのであれば，結果は削除された dnを除いて array と同じ次元の配列である．
  • ArrayReduce[f,array,n1;;n2]とArrayReduce[f,array,{n1,n2,…}]の f は，指定の次元を組み合せて平坦化することで形成されたすべてのベクトルに適用される．
  • ArrayReduce[f,array,{{n11,n12,…},{n21,n22,…},…}]の f はベクトルだけではなく任意次数の配列に適用される．
  • ArrayReduce[f,array,{n1,n2,…}]はArrayReduce[f,array,{{n1,n2,…}}]に等しい．

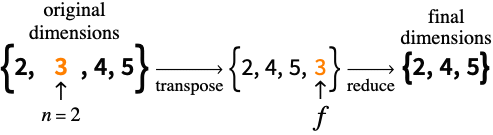
例題

例  (3)

行列のすべての行の平均を計算する：

行列のすべての列の平均を計算する：

次数3の配列を定義する：

2番目の次元についての標準偏差を計算する：

結果の配列は次数2で，2番目の軸は削除された：

入出力配列を可視化する：

次数5の配列を定義する：

次元2と次元4の合計を計算することで配列の次元を削減する：

Wolfram Research (2020), ArrayReduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArrayReduce.html.

テキスト

Wolfram Research (2020), ArrayReduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArrayReduce.html.

CMS

Wolfram Language. 2020. "ArrayReduce." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayReduce.html.

APA

Wolfram Language. (2020). ArrayReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayReduce.html

BibTeX

@misc{reference.wolfram_2024_arrayreduce, author="Wolfram Research", title="{ArrayReduce}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayReduce.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arrayreduce, organization={Wolfram Research}, title={ArrayReduce}, year={2020}, url={https://reference.wolfram.com/language/ref/ArrayReduce.html}, note=[Accessed: 22-November-2024 ]}