Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ArrayFlatten

ArrayFlatten[{{m₁₁,m₁₂,…},{m₂₁,m₂₂,…},…}]

creates a single flattened matrix from a matrix of matrices m_{i j}.

ArrayFlatten[a,r]

flattens out r pairs of levels in the array a.

Details

ArrayFlatten requires that the blocks it flattens have dimensions that fit together.
ArrayFlatten can be used to form block matrices from arrays of blocks.
For a matrix of matrices, ArrayFlatten[a] yields a matrix whose elements are in the same order as in MatrixForm[a].
ArrayFlatten[a] is normally equivalent to Flatten[a,{{1,3},{2,4}}]. »
ArrayFlatten[a,r] is normally equivalent to Flatten[a,{{1,r+1},{2,r+2},…,{r,2r}}].
For a tensor with rank 2r, ArrayFlatten[a,r] gives a tensor with rank r.
In ArrayFlatten[{{m₁₁,m₁₂,…},{m₂₁,m₂₂,…},…}], all the matrices m_{i j} in the same row must have the same first dimension, and matrices m_{i j} in the same column must have the same second dimension.
In general, in ArrayFlatten[a,r], all the k 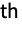dimensions of a[[i₁,i₂,…,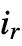]] must be equal for each possible value of i_k.
Elements at level r whose array depth is less than r are treated as scalars, and are replicated to fill out a rank-r array of the appropriate dimensions.
ArrayFlatten works with SparseArray objects. »

Examples

open allclose all

Basic Examples (2)

Create a block matrix by flattening out a matrix of matrices:

Use 0s to represent zero matrices:

Scope (4)

Flatten a rank-4 array to rank 2:

Flatten only the first four levels of a rank-6 array:

Flatten a rank 6 array to rank 3:

ArrayFlatten works with SparseArray objects:

Make a sparse matrix from a block matrix of SparseArray objects:

Applications (5)

Put together many copies of a "tile":

Iterate a 2D substitution system:

Iterate a 3D substitution system:

Form an involutory matrix , such that :

Check that the resulting matrix is involutory:

Form a block matrix semidiscretization of the wave equation with n spatial points:

Differentiation matrix for second-order approximation of with periodic boundary conditions:

Identity matrix of size n:

Form block matrix a for system where :

Identity matrix of size 2 n:

Set up an initial condition vector for :

Approximate the solution at using the backward Euler method with time step k:

Show and at :

Properties & Relations (3)

MatrixForm displays matrices of matrices in the same order as ArrayFlatten:

ArrayFlatten is a special case of Flatten:

KroneckerProduct is defined as ArrayFlatten of an Outer product:

Top