BSplineFunction[{pt1,pt2,…}]
represents a B-spline function for a curve defined by the control points pti.
BSplineFunction[array]
represents a B-spline function for a surface or high-dimensional manifold.


BSplineFunction
BSplineFunction[{pt1,pt2,…}]
represents a B-spline function for a curve defined by the control points pti.
BSplineFunction[array]
represents a B-spline function for a surface or high-dimensional manifold.
Details and Options

- BSplineFunction is also known as basis spline, nonuniform rational B-spline (NURBS).
- BSplineFunction[…][u] gives the point on a B-spline curve corresponding to parameter u.
- BSplineFunction[…][u,v,…] gives the point on a general B-spline manifold corresponding to the parameters u, v, ….
- The embedding dimension for the curve represented by BSplineFunction[{pt1,pt2,…}] is given by the length of the lists pti.
- BSplineFunction[array] can handle arrays of any depth, representing manifolds of any dimension.
- The dimension of the manifold represented by BSplineFunction[array] is given by ArrayDepth[array]-1. The lengths of the lists that occur at the lowest level in the array define the embedding dimension.
- BSplineFunction[array,d] creates a B-spline function of d variables.
- The parameters u, v, … by default run from 0 to 1 over the domain of the curve or other manifold.
- The following options can be given:
-
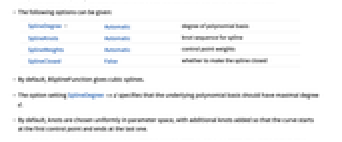
SplineDegree Automatic degree of polynomial basis SplineKnots Automatic knot sequence for spline SplineWeights Automatic control point weights SplineClosed False whether to make the spline closed - By default, BSplineFunction gives cubic splines.
- The option setting SplineDegree->d specifies that the underlying polynomial basis should have maximal degree d.
- By default, knots are chosen uniformly in parameter space, with additional knots added so that the curve starts at the first control point and ends at the last one.
- With an explicit setting for SplineKnots, the degree of the polynomial basis is determined from the number of knots specified and the number of control points.
- With the default setting SplineWeights->Automatic, all control points are chosen to have equal weights, corresponding to a polynomial B-spline function.
- With the setting SplineClosed->{c1,c2,…}, the boundaries are connected in directions i for which ci is True.
Examples
open all close allBasic Examples (2)
Scope (4)
Generalizations & Extensions (1)
SparseArray can be used with BSplineFunction:
Options (6)
SplineDegree (2)
SplineKnots (3)
SplineKnots->Automatic generates knots in such a way that the curve is smooth overall:
By repeating knots, one can decrease the smoothness of the curve:
Uniform knots that do not go through the endpoints:
Unclamped knots combined with SplineClosed will make a uniform periodic B-spline curve:
See Also
BezierFunction InterpolatingFunction BSplineBasis BSplineCurve BSplineSurface Piecewise
Function Repository: CurveToBSplineFunction AkimaInterpolation AkimaSpline LeeInterpolatingNodes
Related Guides
History
Text
Wolfram Research (2008), BSplineFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/BSplineFunction.html.
CMS
Wolfram Language. 2008. "BSplineFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BSplineFunction.html.
APA
Wolfram Language. (2008). BSplineFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BSplineFunction.html
BibTeX
@misc{reference.wolfram_2025_bsplinefunction, author="Wolfram Research", title="{BSplineFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BSplineFunction.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_bsplinefunction, organization={Wolfram Research}, title={BSplineFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/BSplineFunction.html}, note=[Accessed: 09-March-2026]}