BellB
予備知識
- BellBは,ベル数またはベル多項式返す数学関数である.中でも,BellB[n,x]は
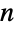
 番目のベル多項式
番目のベル多項式 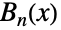 を返し,BellB[n]は
を返し,BellB[n]は 
 番目のベル数
番目のベル数 ![TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2] TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2]](Files/BellB.ja/10.png) を返す.ベル多項式は指数母関数
を返す.ベル多項式は指数母関数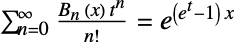 で決定することができる.ベル数は漸化式
で決定することができる.ベル数は漸化式 ![B_(n+1)=sum_(k=0)^nTemplateBox[{n, k}, Binomial]B_k B_(n+1)=sum_(k=0)^nTemplateBox[{n, k}, Binomial]B_k](Files/BellB.ja/12.png) を満足する.最初の数個のベル多項式
を満足する.最初の数個のベル多項式 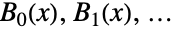 は
は 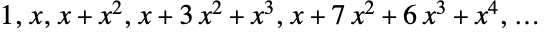 で,最初の数個のベル数
で,最初の数個のベル数 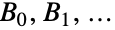 は
は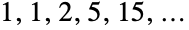 である.
である. - ベル多項式は,指数多項式,あるいはより明示的に,「完全指数ベル多項式」と呼ばれることがあり,
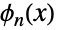 と表示されることがある.ベル多項式は,数学者で数学の解説者でもあり,1934年にこの多項式についての論文を発表したEric Temple Bellに因んで名付けられた.
と表示されることがある.ベル多項式は,数学者で数学の解説者でもあり,1934年にこの多項式についての論文を発表したEric Temple Bellに因んで名付けられた. - 多項式
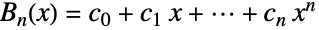 は,
は,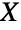 を
を 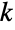 個の部分に分割する方法が
個の部分に分割する方法が 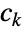 通りあるなら
通りあるなら 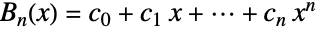 であると解釈される.さらに,
であると解釈される.さらに,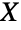 を分割する方法が全部で
を分割する方法が全部で 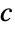 通りなら
通りなら 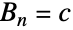 である.例えば,元の数が
である.例えば,元の数が 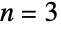 の集合
の集合 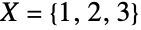 を
を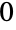 の部分に分割する方法は
の部分に分割する方法は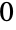 通り
通り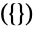 ,
,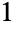 つの部分に分割する方法は
つの部分に分割する方法は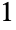 通り (
通り (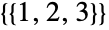 ),
),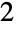 つの部分に分割する方法は
つの部分に分割する方法は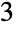 通り(
通り(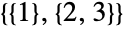 ,
, 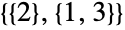 と
と 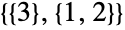 ),
),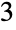 つの部分に分割する方法は
つの部分に分割する方法は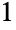 通り(
通り(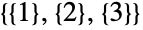 )で,
)で,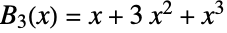 となる.
となる.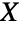 を分割する方法は全部で5通りなので,
を分割する方法は全部で5通りなので,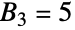 である.
である. - ベル多項式とベル数は,BellY関数の特殊ケース(
![TemplateBox[{n, x}, BellB2]=sum_(k=0)^nY_(n,k)(x,...,x) TemplateBox[{n, x}, BellB2]=sum_(k=0)^nY_(n,k)(x,...,x)](Files/BellB.ja/45.png) および
および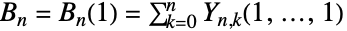 )である.
)である.![TemplateBox[{n, k}, StirlingS2] TemplateBox[{n, k}, StirlingS2]](Files/BellB.ja/47.png) でStirlingS2が返す第2種スターリング数を表すとすると,
でStirlingS2が返す第2種スターリング数を表すとすると,![B_n=B_n(1)=sum_(k=0)^nTemplateBox[{n, k}, StirlingS2] B_n=B_n(1)=sum_(k=0)^nTemplateBox[{n, k}, StirlingS2]](Files/BellB.ja/48.png) となる.
となる.
例題
すべて開くすべて閉じるスコープ (5)
アプリケーション (4)
BellB数とその漸近線との対比:
最初の10個のcomplementary Bell numbersを計算する:
ヘッセンベルグ行列式によるベル数についての式の最初の数例を検証する:
ベル数BellB[n]は,これから作られた2つのハンケル行列式がどちらもBarnesG[n+2]と等しい一意的な集合であるという事実で特徴付けられる.最初のいくつかの例についてこれを検証する:
特性と関係 (7)
BellBの指数型母関数:
PoissonDistributionの ![]() 番目のモーメントは平均
番目のモーメントは平均 ![]() の
の ![]() 番目のBellB多項式で与えられる:
番目のBellB多項式で与えられる:
FullSimplifyを使ってBellBを含む式を簡約する:
IntegerPartitionsを使って指標についての条件を満足する項の総和を直接計算する:
BellBの結果と比較する:
FindSequenceFunctionはBellBを認識する:
考えられる問題 (1)
BellBの第1引数は非負の整数でなければならない:
テキスト
Wolfram Research (2007), BellB, Wolfram言語関数, https://reference.wolfram.com/language/ref/BellB.html.
CMS
Wolfram Language. 2007. "BellB." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BellB.html.
APA
Wolfram Language. (2007). BellB. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BellB.html