BooleanFunction
BooleanFunction[k,n]
変数が n 個である k![]() 次のブール関数を表す.
次のブール関数を表す.
BooleanFunction[values]
真理値の指定されたベクトルに対応するブール関数を表す.
BooleanFunction[{{i11,i12,…}o1,…}]
入力から出力への指定されたマッピングで定義されるブール関数を表す.
BooleanFunction[spec,{a1,a2,…}]
spec で指定されたブール関数に対応する変数 aiのブール式を返す.
BooleanFunction[spec,{a1,a2,…},form]
form で指定された形式のブール式を返す.
詳細


- BooleanFunction[spec]は,Functionのように働くブール関数オブジェクトを返す.
- BooleanFunction[spec][a1,a2,…]は明示的ブール式BooleanFunction[spec,{a1,a2,…}]と等価の暗示的表現を返す.
- BooleanConvertはBooleanFunction[spec][vars]を明示的ブール式に変換する.
- BooleanFunction[values]等では,値はTrueまたはFalseあるいは1または0のどちらかで指定することができる.
- BooleanFunctionで表される関数は常にTrueまたはFalseを返す.
- BooleanFunction[values]では,値は111, … で始まるバイナリ順で指定される.
- BooleanFunction[k,n]はBooleanFunction[IntegerDigits[k,2,2^n]]と等価である.
- BooleanFunction[values]において,各値はベクトル値を持つブール関数を表すリストでもよい.
- BooleanFunction[{{i11,i12,…}->o1,…}]において,oiはベクトル値を持つブール関数を表すリストでもよい.
- 入出力両方の要素を,TrueまたはFalseあるいは1または0のどちらかで指定することができる.
- 入出力両方の要素に「無関係」を表す_の任意の数を入れることができる.
- 入出力両方の要素に連続する「無関係」を表す最高で1個の__を入れることができる.
- BooleanFunction[spec,{a1,a2,…},form]では,可能な形式はBooleanConvertで与えられる.
- BooleanFunction[spec,{a1,a2,…}]は,デフォルトで式を加法標準形(disjunctive normal form, DNF)で与える.
- BooleanFunction[k]は,変数が n 個の k
 次のブール関数を返す.ただし,n は
次のブール関数を返す.ただし,n は 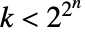 である最小の値を持つ.
である最小の値を持つ. - BooleanFunction[k,…]内のブール関数の付番方式はCellularAutomatonにおけるそれに等しい.
- BooleanFunction[CellularAutomaton[n]]はBooleanFunction[n,3]に等しい.
- BooleanFunction[CellularAutomaton[{n,2,r}]]はBooleanFunction[n,2r+1]に等しい.
- BooleanMinimize,BooleanTable等の操作はBooleanFunctionオブジェクトに直接行うことができる.
- BooleanFunctionオブジェクトは,AndやOr等の他のブール関数と同じように変数に適用することができる.
- StandardFormおよびその関連形式では,BooleanFunctionオブジェクトは変数の数だけが表示された省略形で出力される.
- BooleanVariablesはBooleanFunctionオブジェクトの変数の数を返す.
例題
すべて開くすべて閉じる例 (3)
ブール式をBooleanFunctionに変換する:
スコープ (14)
基本的な用法 (3)
索引を施すことで2引数のBooleanFunctionを作る:
BooleanFunctionは他のブール演算子と同じように使うことができる:
任意のブール式をBooleanFunction式に変換することができる:
BooleanFunction式の組合せを含ませる:
TrueまたはFalseと等価であるBooleanFunction式は自動的に簡約される:
BooleanFunctionは標準表現で,SameQを使って等価性をテストすることができる:
真理値表を使う (7)
これと等価のBooleanFunction式を作る:
対応するBooleanFunction式を作る:
BooleanFunctionを作る:
_と__を使って真理規則の「don't cares」を示す:
BooleanFunctionを作る:
もとの規則は完全に関数を指定し,結果の真理値表は全く等しい:
BooleanFunctionを作る:
BooleanFunctionを作る:
他の表記法を使う (4)
任意のブール式をBooleanFunction式に変換する:
BooleanFunction式を他の標準形式に変換する:
CellularAutomatonを使ってBooleanFunctionを指定する:
アプリケーション (4)
ブール関数の列挙 (2)
新たなプリミティブの作成 (1)
Impliesは x<=y に等しい:
![]() f[u]≤g[u]でありそれ以外ではない場合の,ブール関数 f≼g の関係を定義する:
f[u]≤g[u]でありそれ以外ではない場合の,ブール関数 f≼g の関係を定義する:
すべてのブール関数 f と g について f∧g≼f≼f∨g である:
これは,f∧g⇔f でありそれ以外ではない場合に f≼g であることを証明する:
特性と関係 (7)
省略形で表示されたBooleanFunctionには引数の数が示される:
InputFormはそのオブジェクトの再構築に使うことができる符号化を与える:
与えられた符号化を使ってBooleanFunctionを構築する:
BooleanFunctionの値の順序はBooleanTableのものと等しい:
対応するBooleanFunctionは全く同じ真理値表を持つ:
順序はTuplesと一致する:
BooleanFunctionの指標付けはIntegerDigitsと一致する:
BooleanFunctionから指標に変換する:
指標付きのBooleanFunction式で等価性を示す:
ブール関数の指標付けはセルオートマトンの指標付けに一致する:
より一般的には,整数 ![]() と
と![]() のあるCellularAutomaton[{k,2,r}]について:
のあるCellularAutomaton[{k,2,r}]について:
上記の特性を満足するCellularAutomatonを使ってBooleanFunctionを指定することができる:
BooleanMintermsは任意のBooleanFunctionを表すこともできる:
BooleanConvertを使ってBooleanFunctionを他の形式から変換する:
同じく,BooleanConvertを使ってBooleanFunctionから他の形式に変換する:
BooleanTableを使ってBooleanFunctionから真理値表へ変換する:
テキスト
Wolfram Research (2008), BooleanFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/BooleanFunction.html.
CMS
Wolfram Language. 2008. "BooleanFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BooleanFunction.html.
APA
Wolfram Language. (2008). BooleanFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BooleanFunction.html