WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Or
✖
Or

✖
e1||e2||…

is the logical OR function. It evaluates its arguments in order, giving True immediately if any of them are True, and False if they are all False.

Details

  • Or[e1,e2,…] can be input in StandardForm and InputForm as 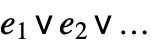e_(1)∨e_(2)∨.... The character 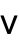∨ can be entered as ||, or, or \[Or].
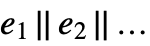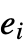  • Or has attribute HoldAll, and explicitly controls the evaluation of its arguments. In e_(1)||e_(2)||... the e_(i) are evaluated in order, stopping if any of them are found to be True.
  • Or gives symbolic results when necessary, removing initial arguments that are False.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Combine assertions with ||:

In[1]:=1
✖
https://wolfram.com/xid/0obok-cfai82
Out[1]=1

A symbolic disjunction:

In[1]:=1
✖
https://wolfram.com/xid/0obok-yi6vv
Out[1]=1

A system of equations:

In[1]:=1
✖
https://wolfram.com/xid/0obok-geut30
Out[1]=1

Enter using or:

In[1]:=1
✖
https://wolfram.com/xid/0obok-cyw7h8
Out[1]=1

Scope  (5)Survey of the scope of standard use cases

Or works with any number of arguments:

In[1]:=1
✖
https://wolfram.com/xid/0obok-hb9gh
Out[1]=1

Or is associative:

In[2]:=2
✖
https://wolfram.com/xid/0obok-d7h0mk

Or with explicit True or False arguments will simplify:

In[1]:=1
✖
https://wolfram.com/xid/0obok-i4iqla
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-j63r74
Out[2]=2

Or evaluates its arguments in order, stopping when an argument evaluates to True:

In[1]:=1
✖
https://wolfram.com/xid/0obok-dmd6x9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-dltf5i
Out[2]=2

The order of arguments may be important:

In[3]:=3
✖
https://wolfram.com/xid/0obok-lu6s7g
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0obok-j8qidu
Out[4]=4

Symbolic transformations will not preserve argument ordering:

In[1]:=1
✖
https://wolfram.com/xid/0obok-k00ay
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-c40ywc
Out[2]=2

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0obok-d2raes

Applications  (6)Sample problems that can be solved with this function

Combine conditions in a Wolfram Language program:

In[1]:=1
✖
https://wolfram.com/xid/0obok-poaj84
In[2]:=2
✖
https://wolfram.com/xid/0obok-jlvdi
Out[2]=2

If an argument of Or evaluates to True, any subsequent arguments are not evaluated:

In[3]:=3
✖
https://wolfram.com/xid/0obok-b6s974
Out[3]=3

The argument order in Or matters; if the last two arguments are reversed, I≥0 is evaluated:

In[4]:=4
✖
https://wolfram.com/xid/0obok-m52z05
In[5]:=5
✖
https://wolfram.com/xid/0obok-f1vek
Out[5]=5

Combine assumptions:

In[1]:=1
✖
https://wolfram.com/xid/0obok-8d9x7
Out[1]=1

Combine equations and inequalities; Or is used both in the input and the output:

In[1]:=1
✖
https://wolfram.com/xid/0obok-p9ndzd
Out[1]=1

Use || to combine conditions:

In[1]:=1
✖
https://wolfram.com/xid/0obok-ctbbhn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-dazood
Out[2]=2

A cellular automaton based on Or:

In[1]:=1
✖
https://wolfram.com/xid/0obok-gddzdp
Out[1]=1

Find the area of the union of sets given by algebraic conditions:

In[1]:=1
✖
https://wolfram.com/xid/0obok-fe4ca9
Out[1]=1

This shows the set:

In[2]:=2
✖
https://wolfram.com/xid/0obok-c14dt7
Out[2]=2

Properties & Relations  (7)Properties of the function, and connections to other functions

Truth table for binary Or:

In[1]:=1
✖
https://wolfram.com/xid/0obok-ib02ro
Out[1]=1

Ternary Or:

In[2]:=2
✖
https://wolfram.com/xid/0obok-cwl4xo
Out[2]=2

Zero-argument Or is False:

In[1]:=1
✖
https://wolfram.com/xid/0obok-9ob000
Out[1]=1

Or with a single argument will return the evaluated argument regardless of value:

In[1]:=1
✖
https://wolfram.com/xid/0obok-g7dcos
Out[1]=1

&& has higher precedence than ||:

In[1]:=1
✖
https://wolfram.com/xid/0obok-lqm1sh

Use BooleanConvert to expand And with respect to Or:

In[1]:=1
✖
https://wolfram.com/xid/0obok-fcn3e0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-kk4ggu
Out[2]=2

De Morgan's laws relate And, Or, and Not:

In[1]:=1
✖
https://wolfram.com/xid/0obok-d8jn2e
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-okqqa7
Out[2]=2

Disjunction of conditions corresponds to the Max of Boole functions:

In[1]:=1
✖
https://wolfram.com/xid/0obok-jec7qu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0obok-yhneo
Out[2]=2
Wolfram Research (1988), Or, Wolfram Language function, https://reference.wolfram.com/language/ref/Or.html (updated 1996).
✖
Wolfram Research (1988), Or, Wolfram Language function, https://reference.wolfram.com/language/ref/Or.html (updated 1996).

Text

Wolfram Research (1988), Or, Wolfram Language function, https://reference.wolfram.com/language/ref/Or.html (updated 1996).

✖
Wolfram Research (1988), Or, Wolfram Language function, https://reference.wolfram.com/language/ref/Or.html (updated 1996).

CMS

Wolfram Language. 1988. "Or." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Or.html.

✖
Wolfram Language. 1988. "Or." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Or.html.

APA

Wolfram Language. (1988). Or. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Or.html

✖
Wolfram Language. (1988). Or. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Or.html

BibTeX

@misc{reference.wolfram_2025_or, author="Wolfram Research", title="{Or}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Or.html}", note=[Accessed: 06-June-2025 ]}

✖
@misc{reference.wolfram_2025_or, author="Wolfram Research", title="{Or}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Or.html}", note=[Accessed: 06-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_or, organization={Wolfram Research}, title={Or}, year={1996}, url={https://reference.wolfram.com/language/ref/Or.html}, note=[Accessed: 06-June-2025 ]}

✖
@online{reference.wolfram_2025_or, organization={Wolfram Research}, title={Or}, year={1996}, url={https://reference.wolfram.com/language/ref/Or.html}, note=[Accessed: 06-June-2025 ]}