BrownianBridgeProcess
BrownianBridgeProcess[σ,{t1,a},{t2,b}]
表示布朗桥过程,从时间 t1 处的数值 a 到时间 t2 处的数值 b,波动率为 σ.
BrownianBridgeProcess[{t1,a},{t2,b}]
表示标准布朗桥过程,从时间 t1 处的数值 a 到时间 t2 处的数值 b.
BrownianBridgeProcess[t1,t2]
表示标准布朗桥过程,在时间 t1 和 t2 处固定为 0.
表示标准布朗桥过程,在时间 0 和时间 1 处固定为 0.
更多信息
- BrownianBridgeProcess 也称为绑定的布朗运动过程.
- BrownianBridgeProcess 是连续时间和连续状态随机过程.
- Brownian bridge 过程的
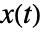 状态满足
状态满足 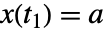 和
和 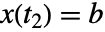 .
. - 状态
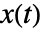 服从 NormalDistribution[a+(b-a) (t-t1)/(t2-t1),
服从 NormalDistribution[a+(b-a) (t-t1)/(t2-t1),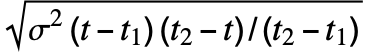 ].
]. - 参数 σ、t1、t2、a 和 b 可以是任意实数,其中 σ 是正数,而 t2 大于 t1.
- BrownianBridgeProcess 可以与诸如 Mean、PDF、Probability 和 RandomFunction 等函数一起使用.
范例
打开所有单元关闭所有单元范围 (13)
基本用法 (8)
过程切片性质 (5)
单变量 SliceDistribution:
二阶 PDF:
CentralMoment 和它的母函数:
对于符号式阶数,FactorialMoment 没有解析形式:
Cumulant 和它的母函数:
属性和关系 (9)
布朗桥过程是一种特殊的 ItoProcess:
也是一种特殊的 StratonovichProcess:
布朗桥过程最初遵循其对应的 WienerProcess:
BrownianBridgeProcess 绝对上确界服从柯尔莫哥洛夫分布:
BrownianBridgeProcess 可以直接从 WienerProcess 模拟:
与相应的 BrownianBridgeProcess 进行比较:
布朗桥是条件 WienerProcess:
文本
Wolfram Research (2012),BrownianBridgeProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html.
CMS
Wolfram 语言. 2012. "BrownianBridgeProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html.
APA
Wolfram 语言. (2012). BrownianBridgeProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BrownianBridgeProcess.html 年