CentralMoment[data,r]
gives the order r![]() central moment
central moment ![]() of data.
of data.
CentralMoment[data,{r1,…,rm}]
gives the order {r1,…,rm} multivariate central moment ![]() of data.
of data.
CentralMoment[dist,…]
gives the central moment of the distribution dist.
represents the order r![]() formal central moment.
formal central moment.


CentralMoment
CentralMoment[data,r]
gives the order r![]() central moment
central moment ![]() of data.
of data.
CentralMoment[data,{r1,…,rm}]
gives the order {r1,…,rm} multivariate central moment ![]() of data.
of data.
CentralMoment[dist,…]
gives the central moment of the distribution dist.
represents the order r![]() formal central moment.
formal central moment.
Details


- CentralMoment is also known as a moment about the mean.
- For scalar order r and data being an array
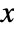 , with mean (first raw moment)
, with mean (first raw moment) 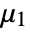 :
: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/CentralMoment.en/8.png)
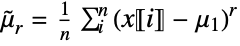
sum of r 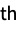 powers »
powers »![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/CentralMoment.en/11.png)
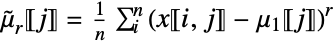
columnwise sum of r 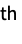 central powers »
central powers »![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/CentralMoment.en/14.png)
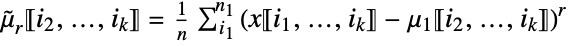
columnwise sum of r 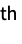 central powers »
central powers » - CentralMoment[x,r] is equivalent to ArrayReduce[CentralMoment[#,r]&,x,1].
- For vector order {r1,…,rm} and data being array
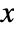 , with first raw moment
, with first raw moment 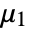 :
: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/CentralMoment.en/19.png)
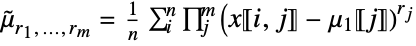
sum the rj 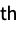 central power in the j
central power in the j column
column![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/CentralMoment.en/23.png)
sum the rj  central power in the j
central power in the j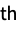 column »
column » - CentralMoment[x,{r1,…,rm}] is equivalent to ArrayReduce[CentralMoment[#,
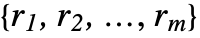 ]&,x,{{1},{2}}].
]&,x,{{1},{2}}]. - CentralMoment handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » WeightedData weighted mean, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channels' values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times » - For a distribution dist, the r
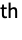 central moment is given by Expectation[(x-Mean[dist])r,xdist]. »
central moment is given by Expectation[(x-Mean[dist])r,xdist]. » - For a multivariate distribution dist, the {r1,…,rm}
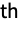 central moment is given by Expectation[(x1-μ1)r1⋯(x2-μm)rm,{x1,…,xm}dist] and {μ1,…,μm}=Mean[dist]. »
central moment is given by Expectation[(x1-μ1)r1⋯(x2-μm)rm,{x1,…,xm}dist] and {μ1,…,μm}=Mean[dist]. » - For a random process proc, the central moment function can be computed for slice distribution at time t, SliceDistribution[proc,t], as
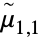 [t]=CentralMoment[SliceDistribution[proc,t],r]. »
[t]=CentralMoment[SliceDistribution[proc,t],r]. » - CentralMoment[r] can be used in functions such as MomentConvert and MomentEvaluate, etc. »
Examples
open all close allBasic Examples (3)
Scope (26)
Basic Uses (6)
Exact input yields exact output:
Approximate input yields approximate output:
Find central moments of WeightedData:
Find a central moment of EventData:
Find a central moment of TimeSeries:
Array Data (5)
For a matrix, CentralMoment gives columnwise moments:
For an array, CentralMoment gives columnwise moments at the first level:
Multivariate CentralMoment for an array:
When the input is an Association, CentralMoment works on its values:
SparseArray data can be used just like dense arrays:
Find the central moment of a QuantityArray:
Image and Audio Data (2)
Channelwise central moment of an RGB image:
Central moment intensity value of a grayscale image:
On audio objects, CentralMoment works channelwise:
Date and Time (4)
Distribution and Process Moments (5)
Scalar central moment for univariate distributions:
Scalar central moment for multivariate distributions:
Joint central moment for multivariate distributions:
Compute a central moment for a symbolic order r:
A central moment may only evaluate for specific orders:
A central moment may only evaluate numerically:
Central moments for derived distributions:
Central moment function for a random process:
Find a central moment of TemporalData at some time t=0.5:
Find the corresponding central moment function together with all the simulations:
Formal Moments (4)
TraditionalForm formatting for formal moments:
Convert combinations of formal moments to an expression involving CentralMoment:
Evaluate an expression involving formal moments ![]() for a distribution:
for a distribution:
Find a sample estimator for an expression involving CentralMoment:
Applications (11)
The first central moment is always 0:
The second central moment is a measure of dispersion:
The third central moment is a measure of skewness:
Estimate parameters of a distribution using the method of moments:
Compare data and the estimated parametric distribution:
Find a normal approximation to GammaDistribution using the method of moments:
Compare an original and an approximated distribution:
Construct a sample estimator of the second central moment:
Find its sample distribution expectation, assuming sample size ![]() :
:
Find sample distribution variance of the estimator:
Variance of the estimator for uniformly distributed sample:
The law of large numbers states that a sample moment approaches population moment as sample size increases. Use Histogram to show the probability distribution of a second sample central moment of uniform random variates for different sample sizes:
Edgeworth expansion for near-normal data correcting for third and fourth central moments:
Function computing sample Jarque–Bera statistics [link]:
Accumulate statistics on samples of normal random variates:
Compare the statistics histogram with an asymptotic distribution:
Compute a moving central moment for some data:
Compute central moments for slices of a collection of paths of a random process:
Properties & Relations (11)
Central moments are translation invariant:
The second central moment is a scaled Variance:
The odd moments of 2×2 matrices vanish:
For a multivariate order, the total order must be odd:
The multivariate central moment of an array of depth ![]() has depth
has depth ![]() :
:
Sqrt of the second central moment is RootMeanSquare of deviations from the Mean:
Skewness is a ratio of powers of third and second central moments:
Kurtosis is a ratio of powers of fourth and second central moments:
CentralMoment is equivalent to an Expectation of a power of a random variable around its mean:
CentralMoment of order ![]() is equivalent to
is equivalent to ![]() when both exist:
when both exist:
Use CentralMoment directly:
Find the central moment–generating function by using GeneratingFunction:
Compare with direct evaluation of CentralMomentGeneratingFunction:
CentralMoment can be expressed in terms of Moment, Cumulant, or FactorialMoment:
Possible Issues (2)
Central moments of higher order are undefined for a heavy-tailed distribution:
Compute central moments on 5 independent samples of the distribution:
Sample central moments of higher order exhibit wild fluctuations:
Sample estimators of central moments are biased:
Find sampling population expectation assuming a sample of size ![]() :
:
The estimator is asymptotically unbiased:
Construct an unbiased estimator:
The expected value of the estimator is the central moment for all sample sizes:
Neat Examples (1)
The distribution of CentralMoment estimates for 20, 100, and 300 samples:
Tech Notes
Related Workflows
- Analyze a Computable Dataset
History
Introduced in 2007 (6.0) | Updated in 2010 (8.0) ▪ 2024 (14.0) ▪ 2024 (14.1)
Text
Wolfram Research (2007), CentralMoment, Wolfram Language function, https://reference.wolfram.com/language/ref/CentralMoment.html (updated 2024).
CMS
Wolfram Language. 2007. "CentralMoment." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/CentralMoment.html.
APA
Wolfram Language. (2007). CentralMoment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralMoment.html
BibTeX
@misc{reference.wolfram_2025_centralmoment, author="Wolfram Research", title="{CentralMoment}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CentralMoment.html}", note=[Accessed: 07-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_centralmoment, organization={Wolfram Research}, title={CentralMoment}, year={2024}, url={https://reference.wolfram.com/language/ref/CentralMoment.html}, note=[Accessed: 07-January-2026]}