CentralMomentGeneratingFunction
✖
CentralMomentGeneratingFunction
詳細
- CentralMomentGeneratingFunction[dist,t]はExpectation[Exp[t(x-μ)],xdist]で与えられる.ただし,μ=Mean[dist]である.
- CentralMomentGeneratingFunction[dist, {t1,t2,…}]はベクトル t と x について,μ=Mean[dist]であるExpectation[Exp[t.(x-μ)],xdist]に等しい.
- i
 次の中心モーメントはSeriesCoefficient[cmgf,{t,0,i}]i!を通して中心モーメント母関数 cmgf から抽出することができる.
次の中心モーメントはSeriesCoefficient[cmgf,{t,0,i}]i!を通して中心モーメント母関数 cmgf から抽出することができる.
例題
すべて開くすべて閉じる例 (3)基本的な使用例
スコープ (5)標準的な使用例のスコープの概要
https://wolfram.com/xid/0yj563omm2s42lwi2q-os0ap2
https://wolfram.com/xid/0yj563omm2s42lwi2q-nbz1my
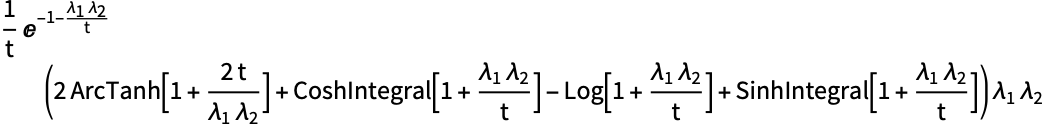
https://wolfram.com/xid/0yj563omm2s42lwi2q-dtx9ye
https://wolfram.com/xid/0yj563omm2s42lwi2q-dms992
https://wolfram.com/xid/0yj563omm2s42lwi2q-0196
ランダム過程のスライス分布についての中心モーメント母関数を求める:
https://wolfram.com/xid/0yj563omm2s42lwi2q-hha5jz
アプリケーション (3)この関数で解くことのできる問題の例
https://wolfram.com/xid/0yj563omm2s42lwi2q-bauyz8
https://wolfram.com/xid/0yj563omm2s42lwi2q-m79nn
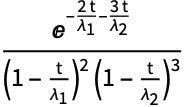
![]() のとき,それはErlangDistributionの中心モーメント母関数と一致する:
のとき,それはErlangDistributionの中心モーメント母関数と一致する:
https://wolfram.com/xid/0yj563omm2s42lwi2q-dvlhhf
TransformedDistributionで確かめる:
https://wolfram.com/xid/0yj563omm2s42lwi2q-bnp4wu
独立同分布に従う ![]() 個の非心
個の非心 ![]() 確率変量の中心モーメントを最初からいくつか求める:
確率変量の中心モーメントを最初からいくつか求める:
https://wolfram.com/xid/0yj563omm2s42lwi2q-cocoup
https://wolfram.com/xid/0yj563omm2s42lwi2q-fvhwwj
ExponentialDistributionを使って中心極限定理を説明する:
https://wolfram.com/xid/0yj563omm2s42lwi2q-hzcxpv
分散が ![]() になるように再スケールされた指数変量の中心モーメント母関数を求める:
になるように再スケールされた指数変量の中心モーメント母関数を求める:
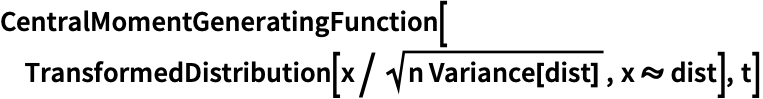
https://wolfram.com/xid/0yj563omm2s42lwi2q-3lqvz
![]() 個のそのような変量の総和の中心モーメント母関数の大きい
個のそのような変量の総和の中心モーメント母関数の大きい ![]() 極限を求める:
極限を求める:
https://wolfram.com/xid/0yj563omm2s42lwi2q-jkzou
https://wolfram.com/xid/0yj563omm2s42lwi2q-pv049t
特性と関係 (3)この関数の特性および他の関数との関係
中心モーメント母関数はモーメント母関数に![]() を掛けたものである:
を掛けたものである:
https://wolfram.com/xid/0yj563omm2s42lwi2q-llpymf
https://wolfram.com/xid/0yj563omm2s42lwi2q-b6eo6n
https://wolfram.com/xid/0yj563omm2s42lwi2q-etcii0
SeriesCoefficientを使って中心モーメント ![]() を求める:
を求める:
https://wolfram.com/xid/0yj563omm2s42lwi2q-h5g8gt
CentralMomentと比較する:
https://wolfram.com/xid/0yj563omm2s42lwi2q-m7hd5
https://wolfram.com/xid/0yj563omm2s42lwi2q-gyk15o
CentralMomentGeneratingFunctionは一連の中心モーメントの指数型母関数である:
https://wolfram.com/xid/0yj563omm2s42lwi2q-blncm1
https://wolfram.com/xid/0yj563omm2s42lwi2q-erfpc8
https://wolfram.com/xid/0yj563omm2s42lwi2q-io1zsa
考えられる問題 (2)よく起る問題と予期しない動作
裾部の長い分布の中には低い次数の中心モーメントがいくつか定義できるだけのものもある:
https://wolfram.com/xid/0yj563omm2s42lwi2q-ftpe5w
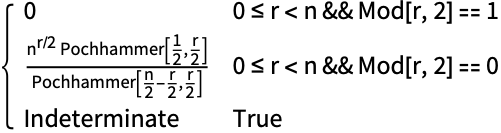
それに相応して,CentralMomentGeneratingFunctionも未定義である:
https://wolfram.com/xid/0yj563omm2s42lwi2q-zyrom
CentralMomentGeneratingFunctionは閉形式では常に既知である訳ではない:
https://wolfram.com/xid/0yj563omm2s42lwi2q-nouwk3
CentralMomentを使って特定の中心モーメントを評価する:
https://wolfram.com/xid/0yj563omm2s42lwi2q-dmrraj
Wolfram Research (2010), CentralMomentGeneratingFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.テキスト
Wolfram Research (2010), CentralMomentGeneratingFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.
Wolfram Research (2010), CentralMomentGeneratingFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.CMS
Wolfram Language. 2010. "CentralMomentGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.
Wolfram Language. 2010. "CentralMomentGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html.APA
Wolfram Language. (2010). CentralMomentGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html
Wolfram Language. (2010). CentralMomentGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.htmlBibTeX
@misc{reference.wolfram_2025_centralmomentgeneratingfunction, author="Wolfram Research", title="{CentralMomentGeneratingFunction}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html}", note=[Accessed: 03-May-2025
]}BibLaTeX
@online{reference.wolfram_2025_centralmomentgeneratingfunction, organization={Wolfram Research}, title={CentralMomentGeneratingFunction}, year={2010}, url={https://reference.wolfram.com/language/ref/CentralMomentGeneratingFunction.html}, note=[Accessed: 03-May-2025
]}