WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

ChineseRemainder

✖
ChineseRemainder[{r1,r2,…},{m1,m2,…}]

gives the smallest with that satisfies all the integer congruences .

✖
ChineseRemainder[{r1,r2,…},{m1,m2,…},d]

gives the smallest with that satisfies all the integer congruences .

Details

  • If no solution for 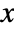exists, ChineseRemainder returns unevaluated.
  • If all 0≤ri<mi, then the result satisfies .
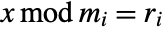  • ChineseRemainder[{r1,r2,…},{m1,m2,…}] gives a solution 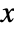with .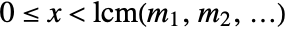
  • ChineseRemainder[{r1,r2,…},{m1,m2,…},d] gives a solution 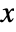with .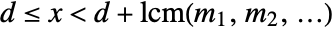

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

The smallest positive integer that satisfies and :

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-gjtp1t
Out[1]=1

Find the smallest positive integer giving remainders when divided by :

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-0czmxj
Out[1]=1

Applications  (3)Sample problems that can be solved with this function

Database encryption and decryption:

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-e7h75m
Out[1]=1

Key generation:

In[2]:=2
✖
https://wolfram.com/xid/0jz78hbdmg1hre-xfx8df
Out[2]=2

Encrypted data:

In[3]:=3
✖
https://wolfram.com/xid/0jz78hbdmg1hre-p1te3c
Out[3]=3

Decryption:

In[4]:=4
✖
https://wolfram.com/xid/0jz78hbdmg1hre-51pfdw
Out[4]=4

Define a residue number system:

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-g55tf1

Numbers and their representation in a residue system:

In[2]:=2
✖
https://wolfram.com/xid/0jz78hbdmg1hre-bp0cku
In[3]:=3
✖
https://wolfram.com/xid/0jz78hbdmg1hre-bje3mp
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0jz78hbdmg1hre-fd6qp
Out[4]=4

Multiplying and recovering in the residue system:

In[5]:=5
✖
https://wolfram.com/xid/0jz78hbdmg1hre-bio07z
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0jz78hbdmg1hre-hsbpfe
Out[6]=6

Adding and recovering:

In[7]:=7
✖
https://wolfram.com/xid/0jz78hbdmg1hre-cayeha
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0jz78hbdmg1hre-i03bzy
Out[8]=8

Modular computation of a determinant:

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-qn5jwv

Modular determinants:

In[2]:=2
✖
https://wolfram.com/xid/0jz78hbdmg1hre-cpf5h4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0jz78hbdmg1hre-ennl9a
Out[3]=3

Recover result:

In[4]:=4
✖
https://wolfram.com/xid/0jz78hbdmg1hre-3ve85
Out[4]=4

Shift residue to be symmetric:

In[5]:=5
✖
https://wolfram.com/xid/0jz78hbdmg1hre-h8q7x6
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0jz78hbdmg1hre-bxv3gt
Out[6]=6

Properties & Relations  (1)Properties of the function, and connections to other functions

Solve congruential equations using Reduce or FindInstance:

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-fp91qf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0jz78hbdmg1hre-mctkp
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0jz78hbdmg1hre-v5ula
Out[3]=3

Possible Issues  (1)Common pitfalls and unexpected behavior

Not all congruential equations have a solution:

In[1]:=1
✖
https://wolfram.com/xid/0jz78hbdmg1hre-cv04q3
Out[1]=1

A solution exists when Mod[ri,GCD[m1,m2,…]]==Mod[rj,GCD[m1,m2,…]]:

In[2]:=2
✖
https://wolfram.com/xid/0jz78hbdmg1hre-bml5na
Out[2]=2
Wolfram Research (2007), ChineseRemainder, Wolfram Language function, https://reference.wolfram.com/language/ref/ChineseRemainder.html (updated 2016).
✖
Wolfram Research (2007), ChineseRemainder, Wolfram Language function, https://reference.wolfram.com/language/ref/ChineseRemainder.html (updated 2016).

Text

Wolfram Research (2007), ChineseRemainder, Wolfram Language function, https://reference.wolfram.com/language/ref/ChineseRemainder.html (updated 2016).

✖
Wolfram Research (2007), ChineseRemainder, Wolfram Language function, https://reference.wolfram.com/language/ref/ChineseRemainder.html (updated 2016).

CMS

Wolfram Language. 2007. "ChineseRemainder." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ChineseRemainder.html.

✖
Wolfram Language. 2007. "ChineseRemainder." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ChineseRemainder.html.

APA

Wolfram Language. (2007). ChineseRemainder. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ChineseRemainder.html

✖
Wolfram Language. (2007). ChineseRemainder. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ChineseRemainder.html

BibTeX

@misc{reference.wolfram_2025_chineseremainder, author="Wolfram Research", title="{ChineseRemainder}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ChineseRemainder.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_chineseremainder, author="Wolfram Research", title="{ChineseRemainder}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ChineseRemainder.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_chineseremainder, organization={Wolfram Research}, title={ChineseRemainder}, year={2016}, url={https://reference.wolfram.com/language/ref/ChineseRemainder.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_chineseremainder, organization={Wolfram Research}, title={ChineseRemainder}, year={2016}, url={https://reference.wolfram.com/language/ref/ChineseRemainder.html}, note=[Accessed: 04-April-2025 ]}