Mod

Mod[m,n]

gives the remainder on division of m by n.

Mod[m,n,d]

uses an offset d.

Details

  • Mod is also known as modulo operation.
  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • Typically used in modular arithmetic, cryptography, random number generation and cyclic operations in programs.
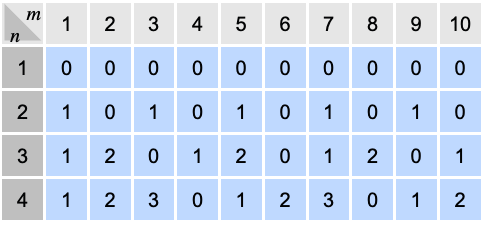
  • Mod[m,n] gives the remainder of m divided by n.
  • Mod[m,n] is equivalent to m-n Quotient[m,n].
  • For positive integers m and n, Mod[m,n] is an integer between 0 and n-1.
  • Mod[m,n,d] gives a result 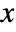such that 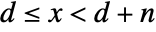and .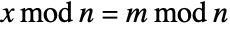

Examples

open allclose all

Basic Examples  (4)

Compute 5 mod 3:

The remainder on division of 5 by 3 offset to start with 1:

Plot the sequence with fixed modulus:

Plot the sequence, varying the modulus:

Scope  (13)

Numerical Evaluation  (6)

Compute using integers:

Compute using an offset:

Mod works on integers:

Rational numbers:

Real numbers:

Complex numbers:

Exact numbers:

Inexact number:

Compute using large integers:

Mod threads over lists:

TraditionalForm formatting:

Symbolic Manipulation  (7)

Solve a modular equation:

Use Mod in a sum:

Product:

Simplify an expression:

Identify Mod sequences:

Recurrence equation:

DirichletTransform:

Generating function:

Applications  (19)

Basic Applications  (3)

The first 20 values of Mod:

Plot the sequence with a fixed modulus:

Plot the sequence, varying the modulus:

Generating function of Mod[n,8]:

Exponential generation function:

Dirichlet series:

Numeric Identifiers  (1)

Given an International Standard Book Number (ISBN), check whether or not it is valid:

An ISBN is valid if , where each is the digit of the ISBN:

Check if each of the ISBNs are valid:

Cryptography  (2)

Build an RSA-like encryption scheme. Start with the modulus:

Find the universal exponent of the multiplication group modulo n:

Private key:

Public key:

Encrypt a message:

Decrypt it:

Use Mod to create a Caesar cipher that shifts letters in the alphabet to encrypt a message:

Encrypt a message with a key:

Decrypt the message:

Number Theory  (6)

Check if numbers of the form are prime or composite:

Select primes below 100 having the form of :

Fermat's little theorem:

Euler's theorem:

Wilson's theorem:

Define a notation for addition modulo 2:

Use Mod to solve systems of linear congruences:

Computer Sciences  (3)

Create a random number generator that uses the current time as a seed:

Choose a modulus and base:

Compute 1000 random numbers between 0 and 1:

Extract parts of a list cyclically:

Modular computation of a matrix inverse:

First compute the matrix adjoint:

Then compute the modular inverse of a matrix:

Check that the inverse gives the correct result:

Politics, Economics and Social Sciences  (2)

Assign memory addresses to social security numbers based on a hashing algorithm:

Assign each social a location, ensuring that there are no collisions:

Compute the result:

Compute the hash of a single social security number:

Other Applications  (2)

Simulate a particle bouncing in a noncommensurate box:

System of 12-tone equal temperament:

Notes that have a difference of 1200 cents are considered to be from the same congruence class:

Properties & Relations  (7)

Mod is a periodic function:

Mod is defined over all complex numbers:

Range:

Mod is transitive. If and , then :

If divides then :

The QuotientRemainder[a,n] is the same as Mod[a,n]:

Use PowerMod to compute the modular inverse:

Check the result:

The results have the same sign as the modulus:

For a positive real number x, Mod[x,1] gives the fractional part of x:

Possible Issues  (1)

Some computations may require higher internal precision than the default:

Reset the value of $MaxExtraPrecision:

Neat Examples  (4)

Binomial coefficients modulo 2:

Additive cellular automaton:

Plot of an Ulam spiral where numbers are colored based on their congruence modulo 49:

Modular addition tables:

Wolfram Research (1988), Mod, Wolfram Language function, https://reference.wolfram.com/language/ref/Mod.html (updated 2002).

Text

Wolfram Research (1988), Mod, Wolfram Language function, https://reference.wolfram.com/language/ref/Mod.html (updated 2002).

CMS

Wolfram Language. 1988. "Mod." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Mod.html.

APA

Wolfram Language. (1988). Mod. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Mod.html

BibTeX

@misc{reference.wolfram_2025_mod, author="Wolfram Research", title="{Mod}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Mod.html}", note=[Accessed: 24-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_mod, organization={Wolfram Research}, title={Mod}, year={2002}, url={https://reference.wolfram.com/language/ref/Mod.html}, note=[Accessed: 24-March-2025 ]}