ChineseRemainder[{r1,r2,…},{m1,m2,…}]
すべての整数合同式 ![]() を満たす
を満たす ![]() の最小の
の最小の ![]() を与える.
を与える.
ChineseRemainder[{r1,r2,…},{m1,m2,…},d]
整数合同式 ![]() を満たす
を満たす ![]() の最小の
の最小の ![]() を与える.
を与える.


ChineseRemainder
ChineseRemainder[{r1,r2,…},{m1,m2,…}]
すべての整数合同式 ![]() を満たす
を満たす ![]() の最小の
の最小の ![]() を与える.
を与える.
ChineseRemainder[{r1,r2,…},{m1,m2,…},d]
整数合同式 ![]() を満たす
を満たす ![]() の最小の
の最小の ![]() を与える.
を与える.
詳細
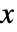 についての解が存在しない場合,ChineseRemainderは未評価のまま返される.
についての解が存在しない場合,ChineseRemainderは未評価のまま返される.- すべてが0≤ri<miであれば,結果は
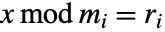 を満たす.
を満たす. - ChineseRemainder[{r1,r2,…},{m1,m2,…}]は
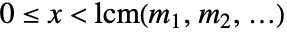 のときの
のときの 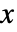 の解を与える.
の解を与える. - ChineseRemainder[{r1,r2,…},{m1,m2,…},d]は
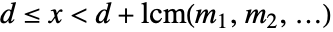 のときの
のときの 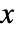 の解を与える.
の解を与える.
テクニカルノート
関連するガイド
-
▪
- ディオファントス(Diophantine)方程式 ▪
- 整数論 ▪
- 整数論関数
テキスト
Wolfram Research (2007), ChineseRemainder, Wolfram言語関数, https://reference.wolfram.com/language/ref/ChineseRemainder.html (2016年に更新).
CMS
Wolfram Language. 2007. "ChineseRemainder." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ChineseRemainder.html.
APA
Wolfram Language. (2007). ChineseRemainder. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ChineseRemainder.html
BibTeX
@misc{reference.wolfram_2025_chineseremainder, author="Wolfram Research", title="{ChineseRemainder}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ChineseRemainder.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_chineseremainder, organization={Wolfram Research}, title={ChineseRemainder}, year={2016}, url={https://reference.wolfram.com/language/ref/ChineseRemainder.html}, note=[Accessed: 07-February-2026]}