ChineseRemainder
ChineseRemainder[{r1,r2,…},{m1,m2,…}]
给出满足所有整数同余式 ![]() 的最小的
的最小的 ![]() (
(![]() ).
).
ChineseRemainder[{r1,r2,…},{m1,m2,…},d]
给出满足所有整数同余式 ![]() 的的最小的
的的最小的 ![]() (
(![]() ).
).
更多信息
- 如果关于
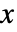 的解不存在,ChineseRemainder 对输入不进行计算,直接返回.
的解不存在,ChineseRemainder 对输入不进行计算,直接返回. - 如果所有的 0≤ri<mi,则结果满足
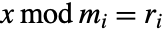 .
. - ChineseRemainder[{r1,r2,…},{m1,m2,…}] 给出解
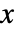 ,同时
,同时 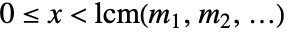 .
. - ChineseRemainder[{r1,r2,…},{m1,m2,…},d] 给出解
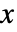 ,同时
,同时 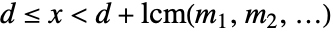 .
.
范例
打开所有单元关闭所有单元
Wolfram Research (2007),ChineseRemainder,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ChineseRemainder.html (更新于 2016 年).
文本
Wolfram Research (2007),ChineseRemainder,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ChineseRemainder.html (更新于 2016 年).
CMS
Wolfram 语言. 2007. "ChineseRemainder." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ChineseRemainder.html.
APA
Wolfram 语言. (2007). ChineseRemainder. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ChineseRemainder.html 年