ClusteringMeasurements

ClusteringMeasurements[{{e1,e2,…},…},meas]

返回聚类样例 ei 的度量 meas.

ClusteringMeasurements[clusters,gt,meas]

假定真实聚类 gt.

更多信息和选项

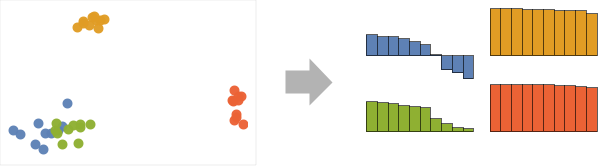
  • ClusteringMeasurements 用于分析聚类过程的结果. 可以单独处理聚类数据，也可以将其与真实信息进行比较.
  • 可能的聚类规范 clusters 包括：
  • {{e1,e2,…},…}聚类样例的列表
    <|l1{e1,e2,…},…|>标签为 li 的聚类样例的关联
    {e1l1,e2l2,…}样例列表及其对应的聚类标签
    {e1,e2,…}{l1,l2,…}分开的样例列表和标签列表
    {e1,e2,…}cfun通过 ClassifierFunction 得到的隐式分类
  • 可能的真实分类规范 gt 包括：
  • {{e1,e2,…},…}示例聚类 (example cluster) 的列表
    <|l1{e1,e2,…},…|>样例列表关联，并用聚类作为标签
    {e1l1,e2l2,…}样例列表及其对应的聚类
    {e1,e2,…}{l1,l2,…}分开的样例和聚类的列表
    {l1,l2,…}每个示例的聚类标签列表
  • 度量 meas 可采用以下形式：
  • "Summary"度量汇总表
    "name"特定度量 "name"
    {"name1","name2",…}度量列表
    All所有可能的度量
    "Properties"可能的度量名称的列表
  • 度量可分为内部度量和外部度量.
  • 内部度量通常假设好的簇具有高分离度和低分散度.
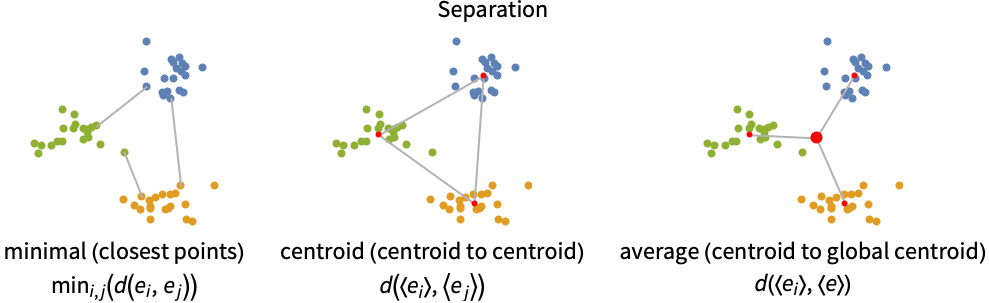
  • 常见的分离度（簇间距离）的定义：
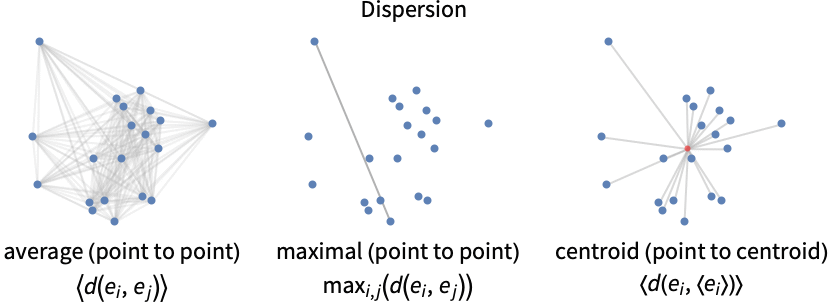
  • 常见的色散（簇内距离）的定义：
  • 符号 〈ei〉 和 〈e〉 表示聚类和整个数据集的平均值.
  • 支持的内部度量 meas 包括：
  • "CalinskiHarabasz"平均分离度和平均质心色散的比值（最大化）
    "DaviesBouldin"一对簇的质心色散和与质心分离度的平均最大比值（最小化）
    "Dunn"最小的最小分离度与数据集最大色散的比值（最大化）
    "RSquared"平均色散的均值与数据集质心色散的比值（肘部法则）
    "Silhouette"簇间距离与最近的簇的簇间距离之间的差的均值（最大化）
    "StandardDeviation"平均色散的均值（肘部法则）
  • 为每个聚类或每个样例返回结果的内部度量包括：
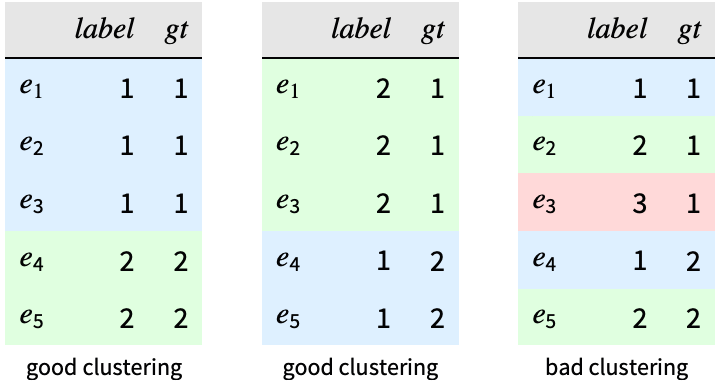
  • "DaviesBouldinScore"最大聚类相似度
    "RSquaredScore"聚类与整个数据集的色散之比
    "SilhouetteScore"簇间距离与最近的簇的簇间距离之间的差
    "SilhouetteScoreList"每个样例的轮廓值
    "StandardDeviationScore"平均色散
  • 外部度量将样例 ei 的聚类分配与其真实值 gt 进行比较.
  • 支持的外部度量包括：
  • "Purity"簇中按最多的真实值分配的样例的比例（最大化）
    "Rand"正确共享或不共享相同的真实值分配的 (ei,ej) 数据对的比例（最大化）
  • 为每个聚类或每个样例返回结果的外部度量包括：
  • "PurityScore"每个簇中共享相同真实值分配的样例的最大比例
    "RandScore"每个簇中正确共享或不共享相同的真实值分配的 (ei,ej) 数据对的比例
  • ClusteringMeasurements[…,{"prop1","prop2",…}] 可用于计算多个属性.
  • ClusteringMeasurements 支持以下选项：
  • DistanceFunction Automatic要使用的距离函数
    FeatureExtractor Identity怎样从样例中提取特征
  • 默认情况下，以下距离函数被用于不同类型的元素：
  • EuclideanDistance数值数据
    ImageDistance图像
    JaccardDissimilarity布尔数据
    EditDistance文本和名义序列
    Abs[DateDifference[#1,#2]]&日期和时间
    ColorDistance颜色
    GeoDistance地理空间数据
    Boole[SameQ[#1,#2]]&名义数据
    HammingDistance名义向量数据
    WarpingDistance数值序列

范例

打开所有单元关闭所有单元

基本范例  (2)

获取聚类度量的汇总：

计算一组聚类的轮廓分数：

用条形图可视化分数：

计算并绘制单个样例的轮廓分数：

范围  (9)

数据格式  (5)

用列表明确指定簇：

用关联明确指定簇：

用样例和分配之间的规则列表指定簇：

用样例和分配之间的规则指定簇：

用样例和 ClassifierFunction[…] 之间的规则指定簇：

度量  (4)

计算聚类属性：

计算一组属性：

计算得出全局度量的汇总：

获取可用属性列表：

指定真实值的情况下获取可用属性列表：

选项  (2)

DistanceFunction  (1)

自定义距离函数：

FeatureExtractor  (1)

自定义特征提取器，对样例进行预处理：

应用  (2)

求合成数据集的最优簇数：

随机排列，合并不同的组：

k 取不同的值，计算 k-均值聚类：

测量每一组聚类的邓恩指数（Dunn index）：

最佳聚类为 5 个聚类：

聚类过程能够恢复所有原始的分组：

可视化聚类中每个点的轮廓图（Silhouette）分数：

计算给定 k 的 k 均值聚类：

可视化 Silhouette 分数：

计算不同 k 值的 k 均值聚类：

用相应的 Silhouette 剖面图绘制每一组聚类：

可能存在的问题  (1)

外部度量需要指定真实值：

互动范例  (1)

对点列表进行聚类以交互方式测量 Calinski–Harabasz 指数：

Wolfram Research (2022)，ClusteringMeasurements，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClusteringMeasurements.html.

文本

Wolfram Research (2022)，ClusteringMeasurements，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClusteringMeasurements.html.

CMS

Wolfram 语言. 2022. "ClusteringMeasurements." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ClusteringMeasurements.html.

APA

Wolfram 语言. (2022). ClusteringMeasurements. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ClusteringMeasurements.html 年

BibTeX

@misc{reference.wolfram_2024_clusteringmeasurements, author="Wolfram Research", title="{ClusteringMeasurements}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ClusteringMeasurements.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_clusteringmeasurements, organization={Wolfram Research}, title={ClusteringMeasurements}, year={2022}, url={https://reference.wolfram.com/language/ref/ClusteringMeasurements.html}, note=[Accessed: 22-November-2024 ]}