Coefficient[expr,form]
gives the coefficient of form in the polynomial expr.
Coefficient[expr,form,n]
gives the coefficient of form^n in expr.


Coefficient
Coefficient[expr,form]
gives the coefficient of form in the polynomial expr.
Coefficient[expr,form,n]
gives the coefficient of form^n in expr.
Details and Options
- Coefficient picks only terms that contain the particular form specified.
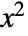 is not considered part of
is not considered part of 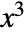 .
. - form can be a product of powers.
- Coefficient[expr,form,0] picks out terms that are not proportional to form.
- Coefficient works whether or not expr is explicitly given in expanded form.
Examples
open all close allScope (4)
Properties & Relations (2)
CoefficientList gives a list of all polynomial coefficients:
The same list of coefficients obtained using Coefficient and Exponent:
For multivariate polynomials CoefficientList gives a tensor of the coefficients:
CoefficientArrays gives the list of arrays of polynomial coefficients ordered by total degree:
In cl the coefficient of x^a y^b is the element at position {a+1,b+1}:
In ca the position of this coefficient is a+b+1 followed by a 1s and b 2s (1 and 2 indicate the first and second variables):
Possible Issues (1)
Coefficient treats transcendental powers as being algebraically unrelated to algebraic powers:
Coefficient treats distinct transcendental powers as being algebraically unrelated to one another:
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0)
Text
Wolfram Research (1988), Coefficient, Wolfram Language function, https://reference.wolfram.com/language/ref/Coefficient.html (updated 1996).
CMS
Wolfram Language. 1988. "Coefficient." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Coefficient.html.
APA
Wolfram Language. (1988). Coefficient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Coefficient.html
BibTeX
@misc{reference.wolfram_2025_coefficient, author="Wolfram Research", title="{Coefficient}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Coefficient.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_coefficient, organization={Wolfram Research}, title={Coefficient}, year={1996}, url={https://reference.wolfram.com/language/ref/Coefficient.html}, note=[Accessed: 24-February-2026]}