ConwayGroupCo2

ConwayGroupCo2[]

散在型単純Conway群Co₂を表す．

詳細

デフォルトで，ConwayGroupCo2[]は点{1,…,2300}に作用する置換群として表される．

予備知識

ConwayGroupCo2[]は，位数がであるConway群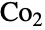を表す．この群は，位数が有限である26の散在型単純群の一つである．ConwayGroupCo2のデフォルト表現は，生成元を2つ持つシンボル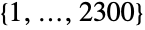上の置換群である．
Conway群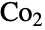は11番目に大きい散在型有限単純群である．この群は1960年代末にJohn Horton Conwayによって導入された．置換表現に加え，ConwayGroupCo2は，いわゆるリーチ(Leech)格子の部分格子を固定するConwayGroupCo1の部分群である．ConwayGroupCo2は，その置換表現に加え，2つの元の体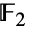上に22次元の忠実表現を持つ．これは，任意の体上の最小の忠実表現である．この群は，生成元によって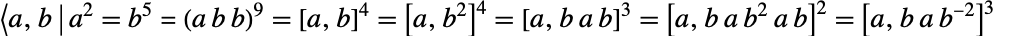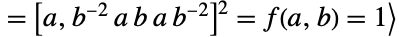，の関係として定義することができる．ただし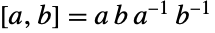，かつ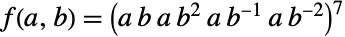である．Conway群は，他の散在型単純群とともに，有限単純群の重要（かつ完全）な分類に大きく貢献した．
ConwayGroupCo2[]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．しかし位数が大きいために，そのような群論関数の数多くは適用されても未評価で返されることがある．Conway群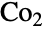の数多くの計算済みの特性を，FiniteGroupData[{"Conway",2},"prop"]を介して得ることができる．
ConwayGroupCo2は他の数多くのシンボルに関連している．ConwayGroupCo2は集合的に散在型有限単純群の「第二世代」と呼ばれる7つの群の一つである（他にConwayGroupCo1，ConwayGroupCo3，JankoGroupJ2，HigmanSimsGroupHS，McLaughlinGroupMcL，SuzukiGroupSuzがある）．この群は，そのすべてがモンスター群のいわゆる部分商として現れる，「Happy」な20個の散在群の一つでもある．