A permutation group defined by two generators:

Compute its order:

An empty list of generators represents the identity (or trivial, or neutral) group:

Find the order of a group generated by two permutations:

Test the equality of permutation groups with the same support but possibly generated by different permutations:

They are different as Wolfram Language expressions:

This is the group of all rotations and reflections of a regular -sided polygon, the dihedral group, for . It can be generated by a rotation of an angle and a reflection along an axis through a vertex:

Construct the octagon corresponding to each group element:

This is the original polygon and its seven rotations. Numbers increase counterclockwise:

This is the polygon reflected along the bisection 1–5 and its seven rotations. Numbers increase clockwise:

The group of automorphisms of a graph is represented using PermutationGroup:

This is the number of automorphisms of the graph:

Explicit representation of a named group:

Generate the symmetric group of degree using transpositions:

Generate the alternating group of degree using generators:

The moves of a Rubik's cube form a group. Number the moving facelets from 1 to 48:

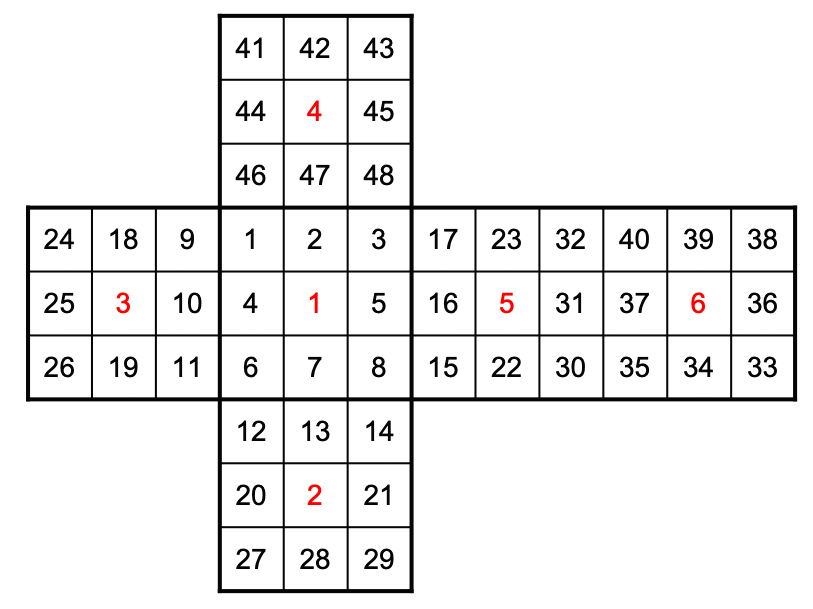
These are the six basic rotations:

Group order:

Swapping two neighbor edge facelets is not allowed:

Simultaneous swaps of two edge pairs is allowed:

This is the superflip move, which switches all edge pairs simultaneously without changing any corner:

Edges and corners cannot be mixed (as the action of the group on the cube is not transitive), but any two corners or any two edges can be swapped: