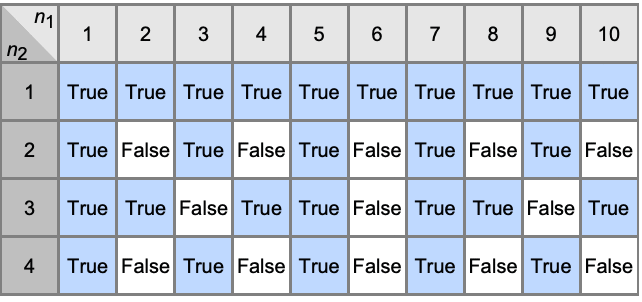
CoprimeQ

CoprimeQ[n1,n2]

n1と n2が互いに素である場合はTrueを，その他の場合はFalseを返す．

CoprimeQ[n1,n2,…]

ni のペアがすべて互いに素である場合はTrueを，その他の場合はFalseを返す．

詳細

  • CoprimeQは，一般的に，2つの数が互いに素かどうかを調べる際に使われる．
  • 整数の最大公約数が1ならそれらの整数は互いに素である．
  • n1,n2が明白に互いに素でなければCoprimeQ[n1,n2]はFalseを返す．
  • GaussianIntegers->Trueのとき，CoprimeQはガウス整数が互いに素かどうかを調べる．
  • CoprimeQはガウス整数に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

2つの数が互いに素かどうかを調べる：

とは互いに素ではない：

スコープ  (4)

CoprimeQは整数に使うことができる：

ガウス整数：

大きい整数について調べる：

CoprimeQは要素単位でリストに縫い込まれる：

オプション  (1)

GaussianIntegers  (1)

が整数上で合成数かどうかを調べる：

ガウス整数：

アプリケーション  (8)

基本的なアプリケーション  (3)

と互いに素な数をハイライトする：

指定された数と互いに素な数をランダムに生成する：

互いに素な数のランダムなペアをプロットする：

2つの数がいつ互いに素になるかを可視化する：

整数論  (5)

CoprimeQを使ってオイラー(Euler)のトーシェント関数を計算する：

CoprimeQを使って自明な最大公約数をチェックする：

最初の個の数のペアの中で互いに素なものの割合を求める：

結果はに近い：

互いに素な数のモジュラ逆数を計算する：

ExtendedGCDを使う：

データベースの暗号化と解読：

鍵の生成：

暗号化されたデータ：

解読されたデータ：

特性と関係  (9)

互いに素な数はに等しい最大公約数GCDを持つ：

互いに素な2つの数の最小公倍数LCMは2つの数の積である：

ある数の約数の数は，互いに素な数については乗算を保持する：

互いに素な a と b は整数 x と y について を満足する：

とはすべての整数と互いに素な唯一の整数である：

素数同士は互いに素である：

EulerPhiは n と互いに素な整数の数を n まで与える：

互いに素な数 a と n は を満足する：

a と b が互いに素なら，と も互いに素である：

おもしろい例題  (2)

互いに素な数をプロットする：

互いに素な数の数列のウラム(Ulam)螺線をプロットする：

Wolfram Research (2007), CoprimeQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoprimeQ.html.

テキスト

Wolfram Research (2007), CoprimeQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoprimeQ.html.

CMS

Wolfram Language. 2007. "CoprimeQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoprimeQ.html.

APA

Wolfram Language. (2007). CoprimeQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoprimeQ.html

BibTeX

@misc{reference.wolfram_2024_coprimeq, author="Wolfram Research", title="{CoprimeQ}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/CoprimeQ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coprimeq, organization={Wolfram Research}, title={CoprimeQ}, year={2007}, url={https://reference.wolfram.com/language/ref/CoprimeQ.html}, note=[Accessed: 22-November-2024 ]}