DGaussianWavelet
represents a derivative of Gaussian wavelet of derivative order 2.
represents a derivative of Gaussian wavelet of derivative order n.
Details
- DGaussianWavelet defines a family of non-orthogonal wavelets.
- The wavelet function (
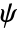 ) is given by
) is given by ![((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2) ((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2)](Files/DGaussianWavelet.en/2.png) .
. - DGaussianWavelet can be used with such functions as ContinuousWaveletTransform, WaveletPsi, etc.
Examples
open allclose allScope (2)
DGaussianWavelet is used to perform ContinuousWaveletTransform:
Use WaveletScalogram to get a time scale representation of wavelet coefficients:
Use InverseWaveletTransform to reconstruct the signal:
Properties & Relations (4)
DGaussianWavelet[2] is the same as MexicanHatWavelet:
Wavelet function integrates to zero; ![]() :
:
Wavelet function and its Fourier transform:
DGaussianWavelet does not have a scaling function:
Text
Wolfram Research (2010), DGaussianWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
CMS
Wolfram Language. 2010. "DGaussianWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
APA
Wolfram Language. (2010). DGaussianWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DGaussianWavelet.html