ContinuousWaveletTransform[{x1,x2,…}]
gives the continuous wavelet transform of a list of values xi.
ContinuousWaveletTransform[data,wave]
gives the continuous wavelet transform using the wavelet wave.
ContinuousWaveletTransform[data,wave,{noct,nvoc}]
gives the continuous wavelet transform using noct octaves with nvoc voices per octave.
ContinuousWaveletTransform[sound,…]
gives the continuous wavelet transform of sampled sound.


ContinuousWaveletTransform
ContinuousWaveletTransform[{x1,x2,…}]
gives the continuous wavelet transform of a list of values xi.
ContinuousWaveletTransform[data,wave]
gives the continuous wavelet transform using the wavelet wave.
ContinuousWaveletTransform[data,wave,{noct,nvoc}]
gives the continuous wavelet transform using noct octaves with nvoc voices per octave.
ContinuousWaveletTransform[sound,…]
gives the continuous wavelet transform of sampled sound.
Details and Options


- ContinuousWaveletTransform gives a ContinuousWaveletData object.
- Properties of the ContinuousWaveletData cwd can be found using cwd["prop"]. A list of available properties can found using cwd["Properties"].
- The resulting wavelet coefficients are arrays of the same dimensions as the input data.
- The possible wavelets wave include:
-
MorletWavelet[…] Morlet cosine times Gaussian GaborWavelet[…] complex Morlet wavelet DGaussianWavelet[…] derivative of Gaussian MexicanHatWavelet[…] second derivative of Gaussian PaulWavelet[…] Paul wavelet - The default wave is MexicanHatWavelet[].
- The default value for noct is given by
![TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor] TemplateBox[{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, {n, /, 2}, )}}, Floor]](Files/ContinuousWaveletTransform.en/1.png) , where
, where 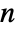 is the length of the input. »
is the length of the input. » - The default value for nvoc is 4.
- The continuous wavelet transform of a function
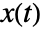 is given by
is given by /s)dt w(u,s)=1/(sqrt(s))int_(-infty)^inftyx(t) TemplateBox[{psi}, Conjugate]((t-u)/s)dt](Files/ContinuousWaveletTransform.en/4.png) .
. - The continuous wavelet transform of a uniformly sampled sequence
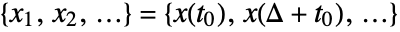 is given by
is given by )/s) w(u,s)=1/(sqrt(s))sum_(k=1)^nx_k TemplateBox[{psi}, Conjugate]((Delta (k-u))/s)](Files/ContinuousWaveletTransform.en/6.png) .
. - The scaling parameter
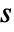 is given by equal-tempered scale
is given by equal-tempered scale 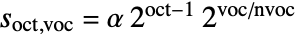 where
where 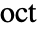 is the octave number,
is the octave number,  the voice number, and
the voice number, and 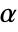 the smallest wavelet scale.
the smallest wavelet scale. - For each scale
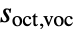 , the ContinuousWaveletTransform computes the wavelet coefficients
, the ContinuousWaveletTransform computes the wavelet coefficients 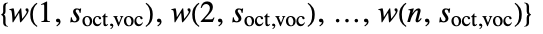 .
. - The following options can be given:
-
Padding None how to extend data beyond boundaries SampleRate Automatic samples per unit WaveletScale Automatic smallest resolvable scale 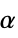
WorkingPrecision MachinePrecision precision to use in internal computations - Padding pads the input data to the next higher power of 2 to reduce boundary effects. The settings for Padding are the same as for the padding argument used in ArrayPad.
- InverseContinuousWaveletTransform gives the inverse transform.
Examples
open all close allBasic Examples (2)
Compute a continuous wavelet transform using MexicanHatWavelet:
Perform an inverse continuous wavelet transform:
Transform a sampled Sound object:
Scope (18)
Basic Uses (6)
Compute a continuous wavelet transform:
Show all the voices for the 8![]() octave:
octave:
Use Normal to get all wavelet coefficients explicitly:
Also use All as an argument to get all coefficients:
Use "IndexMap" to find out what wavelet coefficients are available:
Extract specific coefficient arrays:
Extract several wavelet coefficients corresponding to the list of wavelet index specifications:
Extract all coefficients whose wavelet indexes match a pattern:
WaveletScalogram gives a time scale representation of wavelet coefficients:
More voices per octave increases the scale resolution:
Higher number of octaves gives a wider spectrum of scale range:
Time and Scale Features (4)
A single frequency shows up as a horizontal band at the equivalent scale:
Multiple frequencies show up as multiple bands at the equivalent scales:
Sinusoid with linearly increasing frequency:
Wavelet transform gives a good time localization of features:
Higher frequencies are resolved at lower octaves and lower frequencies at higher octaves:
Resolve time and frequency features of a signal:
Use GaborWavelet to perform a continuous wavelet transform:
There is an inverse relationship between scale values and frequency values:
Find pairs of {oct,voc} that resolve frequencies 20 Hz and 70 Hz:
Verify using a WaveletScalogram:
Wavelet Families (6)
Compute the wavelet transform using different wavelet families:
A narrow wavelet function will have good time and scale resolution:
A broad wavelet function will have poor time and scale resolution:
Use different families of wavelets to capture different features:
MexicanHatWavelet (default):
Sound (2)
ContinuousWaveletTransform works on Sound as input:
Speech analysis using ContinuousWaveletTransform:
The orange patches correspond to the words "You will return safely to Earth":
Options (9)
Padding (3)
SampleRate (3)
For lists, the Automatic value of SampleRate is set to 1:
Explicitly set the sample rate:
For Sound data, the Automatic value of SampleRate is extracted from the Sound data object:
SampleRate is used for normalizing wavelet transform coefficients:
WaveletScale (1)
WaveletScale indicates the smallest resolvable scale used for the transform:
The scales used are given as ![]() with
with ![]() wavelet scale,
wavelet scale, ![]() octave, and
octave, and ![]() voice:
voice:
WorkingPrecision (2)
Applications (4)
Identify Features (2)
Filter Frequencies (2)
ContinuousWaveletTransform can be used to filter frequencies:
Filter the cosine with frequency ![]() :
:
Perform InverseContinuousWaveletTransform on a thresholded data object:
Identify musical notes using a scalogram:
Generate a sequence of pitches corresponding to an equal-tempered scale at 300 Hz:
Compute frequencies resolved corresponding to octaves and voices:
Possible Issues (1)
Low-frequency data is resolved at higher octaves:
Based on the length of input data, the Automatic setting for octaves resolved 8 octaves:
Increase the number of octaves to resolve the low-frequency component:
Neat Examples (1)
Scalogram of a Zeta function:
Related Guides
History
Text
Wolfram Research (2010), ContinuousWaveletTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html.
CMS
Wolfram Language. 2010. "ContinuousWaveletTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html.
APA
Wolfram Language. (2010). ContinuousWaveletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html
BibTeX
@misc{reference.wolfram_2025_continuouswavelettransform, author="Wolfram Research", title="{ContinuousWaveletTransform}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_continuouswavelettransform, organization={Wolfram Research}, title={ContinuousWaveletTransform}, year={2010}, url={https://reference.wolfram.com/language/ref/ContinuousWaveletTransform.html}, note=[Accessed: 10-March-2026]}